Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 138

Seja P um ponto da elipse E : x 2 / a 2 + y 2 / b 2 = 1 .

  1. Suponha que P ≠ B 1 e P ≠ B 2 e considere os pontos R e S de intersecção de O x com as retas B 1 P e B 2 P . Prove que O R → ⋅ O S → = a 2   .
  2. Seja F um foco da elipse. Suponha que P ≠ A 1 e P ≠ A 2 e considere os pontos M e N de interseção da diretriz associada a F com as retas A 1 P e A 2 P . Prove que o ângulo M F ^ N é reto.

Passo 1

  1. Temos o seguinte esquema:

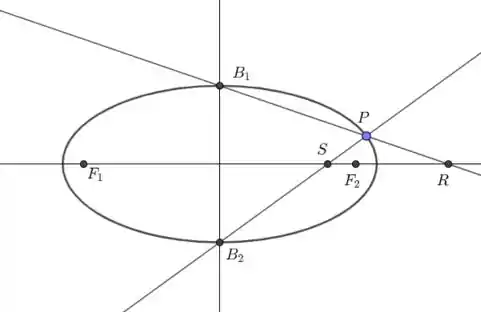
    Seja P = x P ,   y P . Como P é um ponto da elipse, segue que

    x P 2 a 2 + y P 2 b 2 = 1 ⟹ y P = b a a 2 - x P 2

    Vamos calcular as x S e x R .

  • Cálculo de x S : Como B 2 ,   S ,   P são colineares, segue que

    • x S 0 1 0 - b 1 x P y P 1 = 0 ⟹ x S - b - y P + b x P = 0 ∴ x S = b x P b + y P

  • Cálculo se x R : Como B 1 ,   P e R são colineares, segue que:

    • x R 0 1 0 b 1 x P y P 1 = 0 ⟹ x R b - y P - x P b = 0 ∴ x R = b x P b - y P

    Passo 2

    Note que O R → ⋅ O S → = x S ⋅ x R . Vamos então calcular tal produto:

    x S ⋅ x R = b x P b + y P ⋅ b x P b - y P = b 2 x P 2 b 2 - y P 2

    Substituindo o valor de y P :

    x S ⋅ x R = b 2 x P 2 b 2 - b 2 a 2 a 2 - x P 2 = b 2 x P 2 b 2 a 2 a 2 - a 2 + x P 2 = b 2 x P 2 b 2 a 2 ⋅ x P 2 = a 2

    ∴ x S ⋅ x R = a 2

    que é o que queríamos provar!

    Passo 3

  • Temos o seguinte esquema:

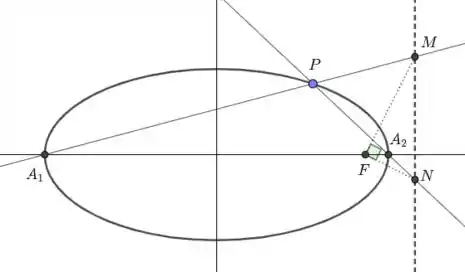
    • Seja F = c , 0 . Sabemos que a reta diretriz associada à F é dada por x = a 2 / c .

    Tomemos A 1 = - a ,   0 e A 2 = a ,   0 e P como definido no item (a).

    Temos que M = a 2 c ,   y M e N = a 2 c ,   y N . Nosso objetivo é calcular y M e y N .

  • Cálculo de y M : Como A 1 ,   P e M são colineares, segue que

    • a 2 c y M 1 - a 0 1 x P y P 1 = 0 ⟹ - a 2 c y P - y M - a - x P - a y P = 0 ∴ y M = y P a + a 2 c a + x P

  • Cálculo de y N : Como A 2 , P e N são colineares, segue que

a 2 c y N 1 a 0 1 x P y P 1 = 0 ⟹ - a 2 c y P - y N a - x P + a y P = 0 ∴ y N = y P a - a 2 c a - x P

Assim,

F N → = N - F = a 2 c , y P a - a 2 c a - x P - c ,   0 = b 2 c , y P a - a 2 c a - x P  

Semelhantemente,

F M → = b 2 c , y P a + a 2 c a + x P

Passo 2

Vamos provar que F N → ⊥ F M → . O jeito mais simples de fazer isso é mostrar que F N → ⋅ F M → = 0 .

Logo,

F N → ⋅ F M → = b 4 c 2 + y P 2 a 2 - a 4 c 2 a 2 - x P 2

Vamos trabalhar um pouco a expressão

y P 2 a 2 - a 4 c 2 a 2 - x P 2 = y P 2 a 2 c 2 - a 2 c 2 a 2 - x P 2 = b 2 a 2 a 2 - x P 2 ⋅ a 2 ⋅ c 2 - a 2 c 2 a 2 - x P 2 = b 2 c 2 - b 2 = - b 4 c 2

Portanto, vemos que

F N → ⋅ F M → = b 4 c 2 + - b 4 c 2 = 0

como queríamos demonstrar!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O arco de uma ponte tem a forma de uma semi-elipse com um vão horizontal de 40 m e com 16 m de altura no centro. Qual a altura do arco a 9 m à esquerda ou à direita do centro?
Para a elipse cuja equação é x - h 2 a 2 + y - k 2 b 2 = 1 Onde ab0 , ache as coordenadas dos focos em termos de h ,k ,aeb .
Uma placa tem a forma da região limitada por uma elipse com semi-eixo maior de 3 cm e com semi-eixo menor de 2 cm. Se a placa for mergulhada verticalmente em um tanque com água até que o eixo menor es
Uma bola de futebol americano tem 30 cm de comprimento e uma secção plana contendo uma costura é uma elipse cujo eixo menor tem 13 cm. Ache o volume da bola se o couro é tão duro que qualquer secção t
Resolva o Exercício 36, se toda secção transversal for uma circunferência.