Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 29

Prove que os pontos 2 ,   4 , 1 ,   - 4 e 5 ,   - 2 são vértices de um triângulo retângulo e acha área do triângulo.

Passo 1

Para saber se o triângulo é retângulo, precisamos encontrar dois lados perpendiculares entre si.

Já para achar sua área, vamos utilizar uma técnica conhecida como “falso determinante”: dados três pontos x 1 ,   y 1 , x 2 ,   y 2 e x 3 ,   y 3 , definimos o falso determinante arranjando as coordenadas em sequência e repetindo o primeiro ponto ao final e multiplicando e somando da seguinte forma:

D = x 1 x 2 x 3 x 1 y 1 y 2 y 3 y 1 = x 1 ⋅ y 2 + x 2 ⋅ y 3 + x 3 ⋅ y 1 - x 2 ⋅ y 1 + x 3 ⋅ y 2 + x 1 ⋅ y 3

E a área do triângulo será

A = D 2

Passo 2

Para começar, vamos marcar os pontos no gráfico.

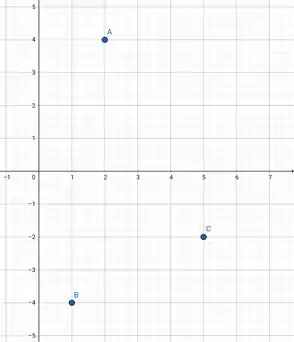
Passo 3

Agora, vamos encontrar as retas-suporte dos lados do triângulo:

Para o lado A B - , y = - 4 - 4 1 - 2 ⋅ x - 2 + 4 = 8 x - 2 + 4 .

Para o lado B C - , y = - 2 - - 4 5 - 1 ⋅ x - 1 - 4 = 1 2 x - 1 - 4 .

Para o lado A C - , y = - 2 - 4 5 - 2 ⋅ x - 2 + 4 = - 2 x - 2 + 4 .

Como 1 2 ⋅ - 2 = - 1 , os lados B C - e A C - são perpendiculares. Logo, o triângulo é retângulo.

Passo 4

Para achar a área, fazemos

D = 2 1 5 2 4 - 4 - 2 4 = 2 ⋅ - 4 + 1 ⋅ - 2 + 5 ⋅ 4 - 1 ⋅ 4 + 5 ⋅ - 4 + 2 ⋅ - 2

D = 30

Passo 5

E finalmente

A = 30 2

A = 15   u .   a .

Resposta

A = 15   u .   a .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Vértices em ( 0 ,5 ) e ( 0 ,- 5 ) e passa pelo ponto 2 , - 5 5 3 .
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Vértices em ( - 2 ,0 ) e ( 2 ,0 ) e passa pelo ponto - 1 , 3 2 .
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Focos em ( 0 ,3 ) e ( 0 ,- 3 ) e a constante mencionada na definição 10.2.1 é 6 3 .
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Vértices em - 5 2 , 0 e 5 2 , 0 e um foco em 3 2 , 0 .
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Centro em ( 4 ,- 2 ) , um vértice em ( 9 ,- 2 ) , e um foco em ( 0 ,- 2 ).