Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 27

Prove que o quadrilátero com vértices 1,2 , 5 ,   - 1 , 11 ,   7 e 7 ,   10 é um retângulo.

Passo 1

Da definição de retângulo, decorre que lados adjacentes são perpendiculares. Basta então provarmos que as retas-suporte de lados adjacentes são perpendiculares.

Passo 2

Para começar, vamos marcar os pontos no gráfico e encontrar as quatro retas suporte.

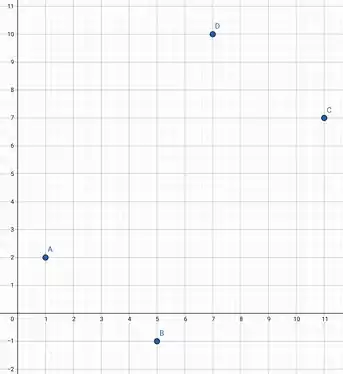
Para o lado A B - , y = - 1 - 2 5 - 1 ⋅ x - 1 + 2 = - 3 4 x - 1 + 2 .

Para o lado B C - , y = - 1 - 7 5 - 1 1 ⋅ x - 1 1 + 7 = 4 3 x - 1 1 + 7 .

Para o lado C D - , y = 7 - 10 11 - 7 ⋅ x - 1 1 + 7 = - 3 4 x - 1 1 + 7 .

Para o lado A D - , y = 10 - 2 7 - 1 ⋅ x - 1 + 2 = 4 3 x - 1 + 2 .

Passo 3

Para saber se são perpendiculares, basta verificar se o produto de seus coeficientes angulares é igual a - 1 :

Entre os lados A B - e   B C - , temos - 3 4 ⋅ 4 3 = - 1 .

Entre os lados B C - e   C D - , temos 4 3 ⋅ - 3 4 = - 1 .

Entre os lados C D - e   A D - , temos - 3 4 ⋅ 4 3 = - 1 .

Entre os lados A D - e   A B - , temos 4 3 ⋅ - 3 4 = - 1 .

Como todos deram - 1 , todas as retas-suporte e, por consequência, todos os lados adjacentes são perpendiculares. Portanto, é um retângulo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Um foco em 2 ,- 3 , um vértice em ( 2 ,4 ) , e centro sobre o eixo x .
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Focos em ( - 5 ,0 ) e ( 5 ,0 ) e a constante mencionada na definição 10.2.1 é 20 .
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Centro na origem, focos sobre o eixo x , o comprimento do eixo maior é três vezes o do eixo menor e passa pelo ponto 3
43. Ao invés de seguir, no sentido inverso, as etapas usadas para obter a equação (8) a partir da equação (1), um método alternativo de obter (1) a partir de (8) é o seguinte: F P - + F ´ P - = x - c
Determine as retas tangentes á elipse E que são paralelas à reta s . aE : 4 x 2 + 2 y 2 = 1 , s : y = 2 x bE : x 2 p + y 2 q = 1 , s : y = m x