Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.1 - Ex. 43
Questão: 43
Ache o centroide da região no primeiro quadrante, limitada pelas curvas e pelo eixo y.
Passo 1
Entendendo o problema
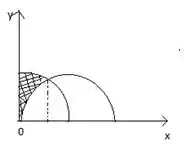
- Primeiro encontraremos a área sobre os gráficos, olhando o gráfico temos que a intersecção ocorre em x = 0 e x = , mas para comprovar fazemos cos x = sen x só ocorre em x = , não é mesmo? Logo esses são os intervalos de integração.
Passo 2
Sabemos que A = = sen x + cos x | =
Para encontrar os componentes do centroide devemos primeiro calcular Área , Mx e My , para encontrar Mx Fazemos;
Mx =
,
e para encontrar My fazemos ;
My = , usando interação por partes, temos ;
Seja
f(x)= x derivando f’(x) = 1
g’(x) = cos x – sen x integrando g(x) = sen x + cos
Passo 3
Então;
My = =
= x (sen x + cos x) | - ( sen x – cos x )
= x (sen x + cos x) - sen x + cos x
Aplicando fica; My =
Logo;
=
=
Resposta
=
=