Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de em , bem como os pontos em que estes valores são atingidos.

1. e o círculo .

Olhando o esboço do gráfico:

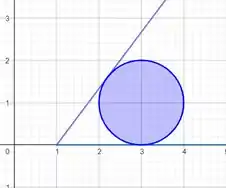
O ponto de mínimo de é porque é a tangente que passa pelo ponto e .

Já o ponto de máximo também tem que passar pelo ponto e tangenciar o círculo.

Aplicando Bhaskara, o :

Assim,

Agora para calcular o ponto em que o valor máximo é atingido:

Jogando agora na equação da reta tangente:

Prontinho!!!