Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.3 - Ex. 28
Se a região na figura gira em torno do eixo para formar um sólido, use a Regra do Ponto Médio com para estimar o volume do sólido.
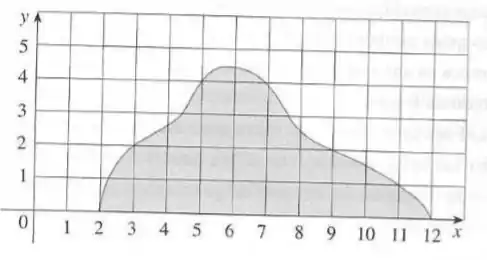
Passo 1
Nosso volume é
Passo 2
Digamos que , onde os valores de são obtidos pelo gráfico. Usando a Regra do Ponto Médio com temos:
Multiplicando esse valor por , que é a parte que falta no cálculo do volume, temos .
Resposta
.
Exercícios de Livros Relacionados
Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir. y = x ,y = - x 2 ,x = 2
Nos Exercícios 1-6, use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
Nos Exercícios 1-6, use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir. y = 2 x ,y = x 2 ,x = 1
Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir. y = x 2 ,y = 2 - x ,x = 0 , p