Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 16
Use integral dupla e encontre a área da região.
A região limitada por ambos as cardioides:
Passo 1
Fala galera, tudo bem? Vamos iniciar mais uma juntos!!!
O enunciado forneceu dois cardioides:
E precisamos determinar a área da região imitada por ambos, através de integral dupla.
Vamos pensar em uma resolução juntos, ok?
Primeiros vamos entender nossa região.
Sabemos que essa figura tem um formato muito parecido com o coração e está escrito em coordenadas polares. Logo, ela tem essa forma:
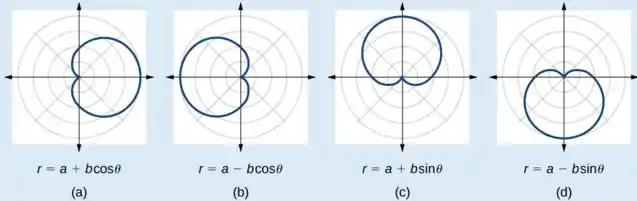
Mas observe que a figura varia conforme a expressão e , e também pelo sinal de e que a expressão tem.
Sabendo disso, podemos fazer um esboço facilmente. Vamos variar o ângulo e aplicar na função de . Desse jeito:
Após determinar nossa região. Podemos aplicar na formula de área em coordenadas polares:
Onde , é a região limitada por ambos os cardioides.
Com essas informações, podemos colocar mão na massa!!! Vamos lá!
Passo 2
Vamos começar pela cardioide:
Agora vamos aplicar os ângulos que mencionamos antes, na expressão acima. Vamos ter:
Agora já temos uma ideia do gráfico, pois calculamos o valor do raio para cada ângulo .
Observe o gráfico feito no Demos, e repare como o raio bate com os valores encontrados acima para cada ângulo:
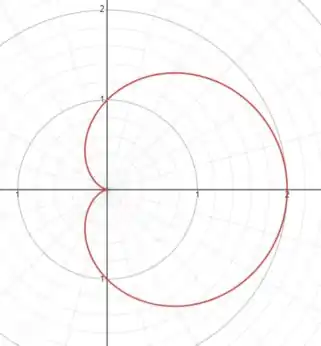
Passo 3
Vamos fazer o mesmo processo do passo 2 para o cardioide:
Agora vamos aplicar os ângulos que mencionamos antes, na expressão acima. Vamos ter:
Já conseguimos ter uma ideia do gráfico, pois calculamos o valor do raio para cada ângulo .
Novamente, observe o gráfico feito no Demos, e repare como o raio bate com os valores encontrados acima para cada ângulo:
Passo 4
Agora vamos unir as dois cardioides e identificar a região limitada por ambos.
Novamente com o auxílio do Demos, vamos ter:
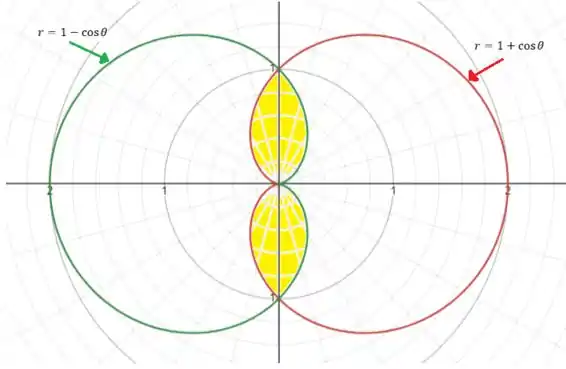
A nossa região de interesse e a região em amarelo.
Agora que conseguimos visualizar a nossa região, vamos utilizar a simetria dela para nos ajudar!
Ao invés de obtermos toda a área de integração, vamos calcular apenas dela. Para isto, basta fazer:
com isto, conseguiremos obter a área da seguinte região:
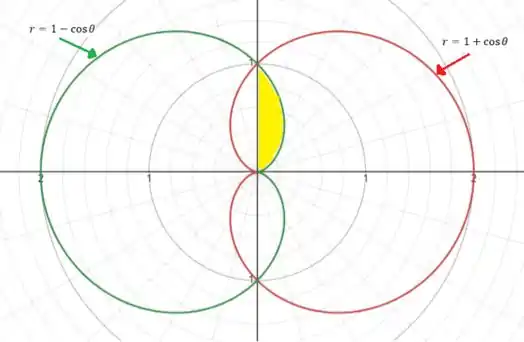
Já sabemos nossa região :
Vamos aplicar na integral dupla:
Desta forma, basta calcular a seguinte integral e multiplica-la por .
Passo 5
Agora, podemos partir para a integração. Mas lembre-se que começamos a integrar de dentro para fora.
Portanto, integrando em vamos ter:
Aplicando dos limites de integração, temos:
Simplificando:
Passo 6
Agora ficamos com uma integral simples em
Sabemos que a integral da soma dos termos é igual a soma das integrais dos termos. Logo, vamos ter:
Simplificando, vamos ter:
Vamos lembrar de uma propriedade trigonométrica, onde:
Vamos ter:
Simplificando:
Agora podemos integrar. Mas lembre-se de aplicar uma substituição na última integral, do tipo:
Logo, vamos ficar com:
Integrando e votando para a variável , temos:
Aplicando os limites de integração, temos:
Simplificando, vamos ter:
Logo, a área é igual a: