Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.3 - Ex. 38

A região limitada pelas curvas dadas é girada ao redor dos eixos especificados. Ache o volume do solido resultante por qualquer método

y = x 2 - 3 x + 2 , y = 0 ; ao redor do eixo x

Passo 1

Inicialmente, vamos analisar o gráfico de nossa x 2 - 3 x + 2 . Então vamos achar as raízes.

x 2 - 3 x + 2 = 0

Logo,

x = 4 ± 9 - 4 ⋅ 1 ⋅ 2 2 → x = 1   o u   x = 2

Então o gráfico fica o seguinte:

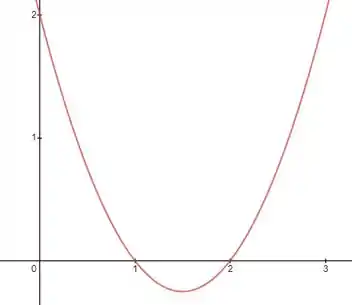
Como queremos rodar ao redor do eixo y a saída mais rápida será usar o método das cascas. Assim,

V = ∫ a b 2 π x f x d x

Como no método das cascas o f x representa o raio e estamos na parte negativa do eixo y , então iremos pegar - f y . Logo,

V = ∫ 1 2 2 π x - x 2 - 3 x + 2 d x

Arrumando as coisas:

V = 2 π ∫ 1 2 - x 3 + 3 x 2 - 2 x d x

Não esquece: ∫ x n d x   = x n + 1 n + 1 + c   quando   n   ≠ - 1

Passo 2

Integrando, temos:

V = 2 π - x 4 4 + 3 x 3 3 - 2 x 2 2 1 2

Isto é,

V = 2 π - x 4 4 + x 3 - x 2 1 2

Aplicando entre esses pontos:

V = 2 π - 2 4 4 + 2 3 - 2 2 - - 1 4 + 1 - 1

Fazendo as contas:

V = π 2

Resposta

V = π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o volume do solido gerado por rotação, em torno do eixo y da região limitada pela curva y = x 4 , a reta x= 1 e eixo x
Ache o volume do sólido gerado se a região do Exercício 25 for rotacionada em torno do eixo y.
Ache o volume do sólido gerado pela rotação da região do Exercício 32 em torno do eixo y.
Ache o volume do sólido gerado pela rotação da região do Exercício 30 em torno da reta x = 2 .
Ache o volume do sólido gerado pela rotação da região limitada pelo gráfico de y = 4 x - 1 8 x 4 , pelo eixo y e pela reta y = 6 em torno da reta x = 2 .