Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 4

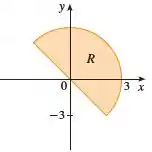
Uma região R é mostrada. Decida se você deve usar coordenadas polares ou retangulares, e escreva ∬ R f x , y d A como uma integral iterada, onde f é uma função qualquer contínua em R .

Passo 1

Fala, pessoal! Tudo de boa?

A questão traz o gráfico de R e quer que a gente escolha se descrevemos essa região com coordenadas polares ou coordenadas retangulares.

As coordenadas retangulares do tipo ( x , y ) são muito úteis para descrever regiões em geral, mas regiões em que temos círculos, setores circulares, por exemplo, são muito complicados de descrever por meio de coordenadas retangulares.

Daí usamos as coordenadas polares que são do tipo:

R = { ( r , θ ) | a ≤ r ≤ b , α ≤ θ ≤ β }

Como no nosso caso temos uma região que se assemelha a um setor circular, vamos escolher usar as coordenadas polares.

Primeiro temos que achar as equações que delimitam a região em coordenadas retangulares e fazer a parametrização para coordenadas polares usando:

x = r   c o s θ

y = r   s e n θ

d A = r   d r   d θ

Por fim, vamos escrever:

∬ R f ( x , y ) d A

Usando como limite de integração o sistema de coordenadas polares.

Mão na massa!

Passo 2

Bom, pessoal, aqui vamos usar as coordenadas polares. Primeiro de tudo, vamos parametrizar x e y :

x = r cos ⁡ θ

y = r sen ⁡ θ

Portanto, a reta que delimita nossa região circular R :

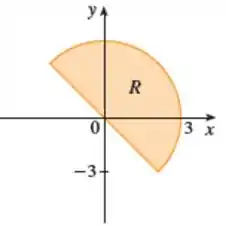
Temos meio círculo limitado por uma reta. Olhando o desenho vemos que a reta está passando no meio dos quadrantes e os dividindo em partes iguais, e que os valores de y são iguais aos valores de x , mas com sinais trocados, então teremos a reta:

y = - x

  • Para o ângulo, podemos usar o eixo x como referência. Os ângulos que saem dele no sentido horário são considerados negativos e no sentido anti-horário, positivos. Partindo do eixo x no sentido horário para a reta y = - x , temos meio quadrante. Um quadrante é π 2 e meio quadrante vai ser π 4 . Como estamos no sentido horário, será - π 4 .

    • Do eixo x até a outra extremidade do semicírculo, temos um quadrante e meio, portanto π 2 + π 4 = 3 π 4 , positivo, já que foi medido no sentido anti-horário.

  • Para o raio r os limites de integração serão de 0 a 3 , já que se trata de uma parte de círculo com origem em 0 e raio igual a 3.

Então nossa região R será em coordenadas polares:

R = { ( r , θ ) | 0 ≤ r ≤ 3 , - π 4 ≤ θ ≤ 3 π 4 }

Logo,

∬ R f ( x , y ) d A = ∫ - π 4 3 π 4 ∫ 0 3 f r cos ⁡ θ , r sen ⁡ θ   r   d r   d θ

Resposta

A integral dupla pode ser escrita como:

∬ R f ( x , y ) d A = ∫ - π 4 3 π 4 ∫ 0 3 f r cos ⁡ θ , r sen ⁡ θ   r   d r   d θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pulverizador agrícola distribui água em um padrão circular de 50m de raio. Ele fornece água até uma profundidade de e - r metros por hora a uma distância de r metros do pulverizador.Se 0R ≤ 50 , qu
Um pulverizador agrícola distribui água em um padrão circular de 50m de raio. Ele fornece água até uma profundidade de e - r metros por hora a uma distância de r metros do pulverizador.Se 0R ≤ 50 , qu
A região dentro do círculo (x - 1)^2 + y^2 = 1 e fora do círculo x^2 + y^2 = 1 .
Expresse a integral dupla em termos de uma integral unidimensional com relação a r . Em seguida, use a calculadora para avaliar a integral correta com quatro casas dimensionais. ∬ D e x 2 + y 2 2 d A
Expresse a integral dupla em termos de uma integral unidimensional com relação a r . Em seguida, use a calculadora para avaliar a integral correta com quatro casas dimensionais. ∬ D x y 1 + x 2 + y 2