Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 2
Uma região é mostrada. Decida se você deve usar coordenadas polares ou retangulares, e escreva como uma integral iterada, onde é uma função qualquer contínua em .
Passo 1
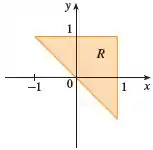
Vamos lá meu amigo, primeiramente precisamos decidir se utilizaremos coordenadas polares ou retangulares para resolver uma integral delimitada pela seguinte região:
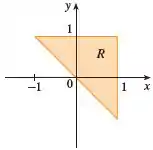
Após isso, precisamos escrever de fato a integral interada. Agora eu quero te perguntar uma coisa. Para que serve as coordenadas polares? Bom, as coordenadas polares servem para faciliar a solução de casos que se tornem muito complicados de serem resolvidos utilizandos as coordenadas retangulares. Ou seja, a não ser que algo te mostre que haverá muita manipulação algébrica utilizando coordenadas retangulares, não há motivo para utilizar as polares. Quer outra dica? Fique atento à esse pulo do gato então:
Em geral, utilizamos coordenadas polares quando pelo menos uma das funções associadas a região for circular ou curvas, pois isso dificultará a solução pelo método tradicional(retangulares).
Passo 2
Escrevendo integral utilizando coordenadas retangulares. Podemos ver pelo desenho que o valor de varia de a .
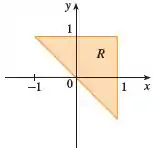
Já o valor de varia da reta até a reta .
Veja que a reta será nosso limite interior, pois estamos fazendo uma região do tipo , em que a integral vai “varrer” a região de baixo para cima.
Então temos nossos limites de integração como:
Como é uma região do tipo , será a integral de “dentro”.
Passo 3
Também podemos resolver utilizando uma região do tipo . Nesse caso diríamos que:
E
“Varrendo” a região horizontalmente. Oque nos daria a seguinte integral interada.
Resposta
A integral dupla pode ser escrita de duas maneiras: