Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 4.4 - Ex. 6

6. Em relação ao sistema de coordenadas cartesianas, uma pessoa esta na origem, no interior de uma praça cujo contorno tem por equação

3 x 2 + 4 x y + 6 y 2 = 140

A que ponto a pessoa deve se dirigir, ao sair da praça, para caminhar o menos possivel

Passo 1

Oii, vamos agora treinar o método dos multiplicadores de Lagrange que consiste em fazer um sistema

∇ f x , y = λ ∇ g

g x , y

Onde f é a nossa função e g é nossa região. Sendo λ nosso multiplicador de Lagrange. Basicamente vamos analisar os pontos onde

∇ f x , y = 0,0

E também onde os pontos que encontrarmos no sistema do método de Lagrange. Bora cair dentro!

Passo 2

O que vamos fazer é o seguinte, nossa praça tem o seguinte formato

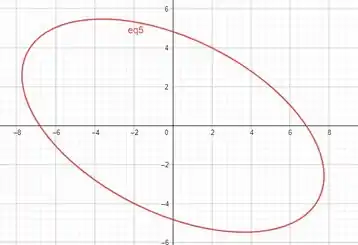
Uma elipse torta. Vamos criar um círculo na origem e achar os pontos de interseção da elipse com o nosso círculo de raio ainda desconhecido. Então nossa função f será

f   x , y :     x 2 + y 2 - a 2 = 0

Onde a é o raio do nosso círculo. Abaixo podemos ver graficamente o que faremos

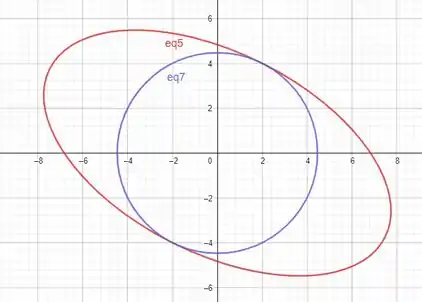
Então nossa função gradiente é

∇ f = 2 x   ,   2 y

Agora vamos calcular agora o gradiente de g

g   :   3 x 2 + 4 x y + 6 y 2 - 140 = 0

∇ g = 6 x + 4 y , 4 x + 12 y

Vamos agora montar o sistema

2 x = λ 6 x + 4 y

2 y = λ 4 x + 12 y

3 x 2 + 4 x y + 6 y 2 - 140 = 0

Podemos ajeitar esse sistema e eliminar uns fatores inúteis

x = λ 3 x + 2 y

y = λ 2 x + 6 y

3 x 2 + 4 x y + 6 y 2 - 140 = 0

Agora sim!

Passo 3

Vamos isolar λ na equação I

λ = x 3 x + 2 y

Agora vamos usar esse valor na equação II

y =   x 3 x + 2 y 2 x + 6 y

Ajeitando essa função ficamos com

2 x 2 - 2 y 2 + 3 x y = 0

Os pontos onde essa função faz interseção com g são os pontos máximos e mínimos da nossa função. Entao agora temos um novo sistema

2 x 2 - 2 y 2 + 3 x y = 0

3 x 2 + 4 x y + 6 y 2 - 140 = 0

Isolando x² na nova equação I teremos

x 2 = y 2 - 3 2 x y

Vamos substituir isso na equação II 3 y 2 - 3 2 x y + 4 x y + 6 y 2 - 140 = 0  

- 1 2 x y + 9 y 2 - 140 = 0

x = - 280 + 18 y 2 y

Show!!! Isolamos x . Vamos voltar com esse valor em g novamente e descobrir agora os pontos de y que resolvem nosso sistema

3 - 280 + 18 y 2 y 2 + 4 y - 280 + 18 y 2 y + 6 y 2 - 140 = 0

3 280 2 - 2 ⋅ 18 ⋅ 280 y 2 + 18 2 y 4 + 4 y 2 - 280 + 18 y 2 + 6 y 2 - 140 = 0

Resolvendo esse problema chegamos aos seguintes pontos

y =   ± 14

y =   ± 4

Se voltarmos a função que achamos de x com esses valores de y encontraremos

x = ± - 280 + 18 4 2 4

x =   ± 2

OU

x =   ± - 280 + 18 14 14

x =   ∓ 7.5

Com isso ficamos com os seguintes pontos

7.5 , - 14  

- 7.5 , 14

2,4

- 2 , - 4

Todos esses pontos fazem interseção. Se formos ver o tamanho da distância entre a Origem (0,0) e os pontos é perceptível que os pontos

2,4  

- 2 , - 4

São o menor caminho. Nossos pontos de mínimos. E os pontos

7.5 , - 14  

- 7.5 , 14

São os pontos de distância máxima. Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

Pontos de distancia minima

2,4  

- 2 , - 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 57 a 61, determinar os pontos de máximo e/ou mínimo da função dada, sujeita às restrições indicadas:57) z = 4 - 2 x - 3 y ;x 2 + y 2 = 1
Precisa-se construir um tanque com a forma de um paralelepípedo para estocar 270 m³ de combustível, gastando a menor quantidade de material em sua construção. Supondo que todas as paredes serão feitas
Nos exercícios 57 a 61, determinar os pontos de máximo e/ou mínimo da função dada, sujeita às restrições indicadas:60) z = x y ;2 x 2 + y 2 = 1 6
Encontre o máximo e mínimo de f x , y = x + y 2 na região D = x , y ∈ R 2 ,x - 2 2 + y 2 ≤ 1
2. Um disco plano tem a forma da região do plano xy definida por x 2 + y 2 ≤ 1 Aquece-se o disco (inclusive a fronteira, onde x 2 + y 2 = 1 ) de modo que a temperatura em cada ponto é dada por T x , y