Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 56
Precisa-se construir um tanque com a forma de um paralelepípedo para estocar 270 m³ de combustível, gastando a menor quantidade de material em sua construção. Supondo que todas as paredes serão feitas com o mesmo material e terão a mesma espessura, determinar as dimensões do tanque.
Passo 1
Beleza galera, neste caso nós temos um problema de otimização restrita, ou seja, queremos encontrar o valor mínimo para as dimensões do paralelepípedo capaz de estocar 270 m³.
Então neste caso a condição será:
Agora precisamos montar a função a ser minimizada, ok?
Para achar as dimensões nós precisamos achar a área total, mas antes vamos ver a caixa:
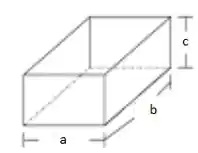
A equação será então:
Como queremos minimizar a área, nós teremos o seguinte problema de otimização:
Passo 2
Colocando na fórmula de Lagrange:
Derivando L em relação às variáveis a, b e c e igualando as derivadas a zero:
Igualando as duas primeiras equações nós achamos:
Se igualamos a segunda e a terceira achamos:
Colocando na última equação:
Achando b e c:
Sendo assim, a dimensão do paralelepípedo é
Tranquilinha?