Repita o Exercício 47 para a curva .
Passo 1
Pessoal, nessa questão devemos encontrar a área acima do eixo para a curva:
Para isso, vamos usar um software gráfico para encontrar quais são os pontos de interseção dessa curva com o eixo .
Sabendo esses pontos, vamos chama-los de e . Temos que a área delimita pela função e o eixo pode ser encontrada a partir de:
Aí basta integrar a função e substituir os limites de integração.
Para encontrar a integral da função, vamos usar a propriedade de que a soma/subtração dentro da integral é a soma/subtração de integrais:
E para encontrar as integrais vamos usar as antiderivadas.
A antiderivada da potência de é dada por:
E também teremos a função:
Aí, temos que saber qual função que quando derivada resulta nesse cara aí de cima.
Para isso, vamos usar as derivadas das inversas trigonométricas:
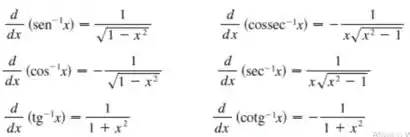
Bom, daí dá pra ver que a função que queremos é a o Arcotangente ().
Passo 2
Através de um software gráfico, temos que o gráfico da função dada é:
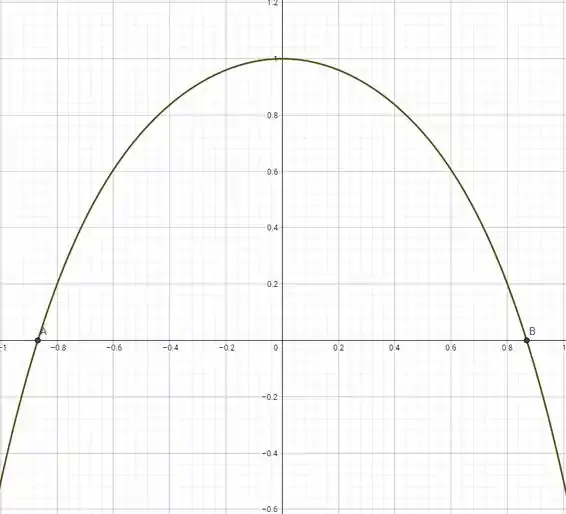
Passo 3
Através do gráfico encontrado, temos que a interseção da curva com o eixo é dada por:
E
Assim, a área pedida é dada por:
Passo 4
Sepando os integrandos para melhor visualização temos:
Integrando temos:
Passo 5
Substituindo os valores aproximados de e , temos que
Resposta
A área aproximada abaixo da curva dada, considerando os extremos
e
é