Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 11.Exercícios - Ex. 319
Resolva no conjunto dos números reais a equação
Passo 1
Opa galerinha, tudo certo?
Para resolver essa equação vamos utilizar a equação dada e a equação da relação fundamental da trigonometria. Iremos começar substituindo essas funções trigonométricas por variáveis para ajudar na visualização e não nos perdemos. Após isso, encontrada a solução precisamos lembrar de voltar aos termos iniciais da questão.
Abaixo temos o ciclo trigonométrico para ajudar na visualização.
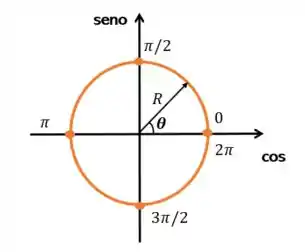
Simbora!
Passo 2
Vamos substituir o seno e o cosseno por duas variáveis.
Adotando:
Lembrando que a relação fundamental da trigonometria é dada por:
Então,
Utilizando nossa substituição:
Isolando na 1ª equação e substituindo-o na 2ª equação, temos:
Simplificando por 2 a equação e colocando em evidência:
Assim, temos dois valores de que fazem essa igualdade ser verdadeira. São eles:
Então, a solução engloba essas duas situações.
Para , o valor de será:
Para , o valor de será:
Passo 3
Beleza, agora precisamos voltar a incógnita inicial do problema. Lembrando que:
Para a 1ª situação:
Para a 2ª situação:
Agora sim, terminamos a questão. Uhuuull!