Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.3 - Ex. 23

(a) Resolva a equação diferencial y ' = 2 x 1 - y 2   .

(b) Resolva o problema de valor inicial y ' = 2 x 1 - y 2 , y 0 = 0 e faça um gráfico da solução.

(c) O problema de valor inicial y ' = 2 x 1 - y 2 , y 0 = 2 tem solução? Explique.

Passo 1

(a) Pessoal, vamos escrever a equação da seguinte forma e verificar que ela é separável:

d y d x = 2 x 1 - y 2

1 1 - y 2 d y = 2 x   d x

Agora integra de cada lado:

∫ 1 1 - y 2 d y = ∫ 2 x   d x + C

a r c s e n y = x 2 + C

Aplicando a função inversa de a r c s e n (que é s e n ), a gente obtém nossa resposta:

y = s e n x 2 + C   ,

respeitando a seguinte condição:

    - π 2 ≤ x 2 + C ≤ π 2   ,

pois a função a r c s e n y só está definida nesse intervalo.

Passo 2

(b) Para resolver o problema de valor inicial, já temos a maior parte do caminho andado, pois encontramos y em função de x no item anterior. Agora, como y 0 = 0 , a gente substitui os valores x = y = 0   na equação encontrada pra achar a constante C :

0 = s e n 0 2 + C

0 = s e n   C

C = 0

Então ficamos com:

y = s e n x 2   ,

respeitando a condição:

- π 2 ≤ x 2 ≤ π 2   ,         o u   s e j a ,         - π 2 ≤ x ≤ π 2     .

Passo 3

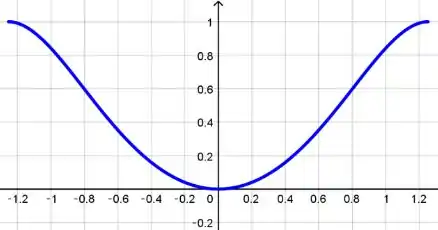
Agora galerinha, pra fazer o gráfico, basta pegar o gráfico da função y = s e n x 2   ,   restrito ao domínio (ou aos valores de x ) : - π 2 ≤ x ≤ π 2     .

Isso quer dizer que a gente vai pegar o gráfico aproximadamente entre os valores de -1,25 e 1,25 para x :

Passo 4

(c) Para verificar a solução do problema de valor inicial descrito neste item, jogamos o valor de x = 0     e     y = 2   , na equação encontrada no item (a) :

y = s e n x 2 + C

2 = s e n 0 2 + C

2 = s e n   C

Mas atenção, pessoal, a função seno só dá valores entre - 1 e 1 , então é impossível existir qualquer constante C que satisfaça esse problema.

Logo, o problema não tem solução, beleza pessoal?

Resposta

a) y = s e n x 2 + C   ,     c o m         - π 2 ≤ x 2 + C ≤ π 2   .

b) y = s e n x 2   ,       c o m       - π 2 ≤ x ≤ π 2 .

c) Não tem solução.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os gráficos das funções logísticas (Figuras 2 e 3 ) são extremamente similares ao gráfico da função tangente hiperbólica (Figura 3 na Seção 3.11 ). Explique a similaridade, mostrando que a função logí
Em um modelo de crescimento sazonal, uma função periódica do tempo é introduzida para considerar variações sazonais na taxa de crescimento. Essas variações podem, por exemplo, ser causadas por mudança
Existe evidência considerável para apoiar a teoria de que, para algumas espécies, existe uma população mínima m de forma que as espécies se tornarão extintas se o tamanho da população cair abaixo de m
Vamos modificar a equação logística do Exemplo 1 como a seguir: d P d t = 0,08P 1 - P 1000 - 15 (a) Suponha que P t represente uma população de peixes no instante t , onde t é medido em semanas. Expli
Suponha que alteremos a equação diferencial no Exercício 19 como a seguir: d P d t = k P cos 2 ⁡ r t - ϕP 0 = P 0 (a) Resolva essa equação diferencial com a ajuda de uma tabela de integrais ou um SCA.