Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.4 - Ex. 24

Suponha que alteremos a equação diferencial no Exercício como a seguir:

(a) Resolva essa equação diferencial com a ajuda de uma tabela de integrais ou um SCA.

(b) Trace a solução para vários valores de e . Como os valores de e afetam a solução? O que você pode dizer sobre nesse caso?

Passo 1

(a) Pessoal, com a ajuda de um SCA, resolvemos a equação diferencial do enunciado:

Passo 2

(b) Agora a gente traça a solução para alguns valores de e :

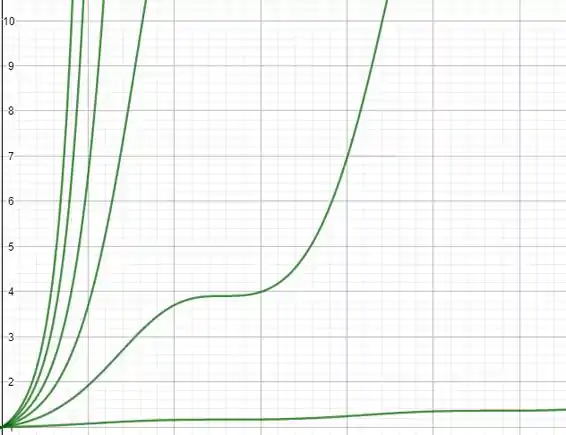
Aqui alteramos somente o valor de : à medida que aumenta, a função oscila menos e tende a se parecer mais com a função exponencial

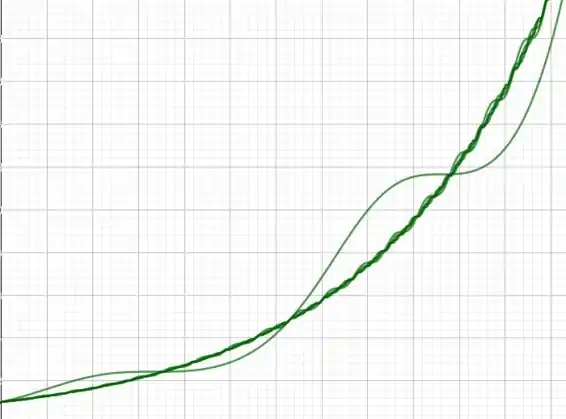
Aqui alteramos somente o valor de : à medida que aumenta, o período parece diminuir

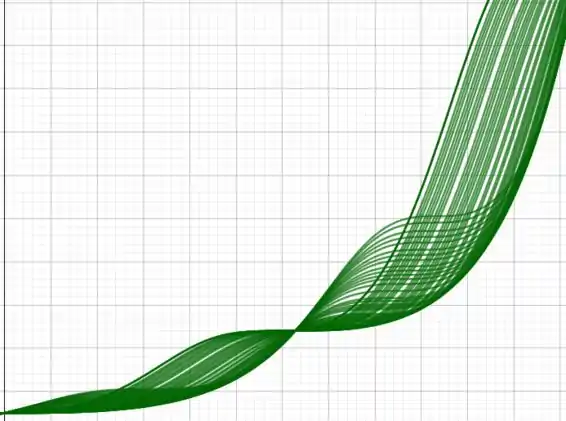
Aqui alteramos somente o valor de : ficou doido né!

Passo 3

Show! Agora vamos calcular o limite:

Realmente, isso condiz bastante com nossos gráficos!

Resposta

(a)

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um habitante comum do intestino humano é a bactéria Escherichai coli. Uma célula dessa bactéria em um meio nutriente se divide em duas células a cada 20 minutos. A população inicial da cultura é de 60

O bistmuto-210 tem uma meia-vida de cinco dias.a) Se uma amostra tem massa de 800m g , encontre uma fórmula para a massa que restará depois de t dias.b) Calcule a massa depois de 30 dias.c) Quando a m

A taxa de mudança da pressão atmosférica P em relação à altitude h é proporcional a P , desde que a temperatura seja constante. A 15° C a pressão é 101,3k P a ao nível do mar e 87,14k P a a h = 1000m

Considere uma população P = P ( t ) com taxas de natalidade e mortalidade relativas constantes α e β , respectivamente, e uma taxa de emigração constante m , onde α , β e m são constantes positivas. A

Uma cultura de bactérias cresce com uma taxa de crescimento relativo constante. A contagem era 600 depois de duas horas e 75000 depois de oito horas.a) Qual a população inicial da cultura?b) Encontre