Vamos modificar a equação logística do Exemplo como a seguir:
(a) Suponha que represente uma população de peixes no instante , onde é medido em semanas. Explique o significado do termo
(b) Desenhe um campo de direções para essa equação diferencial.
(c) Quais são as soluções de equilíbrio?
(d) Use o campo de direções para esboçar várias curvas solução. Descreva o que acontece à população de peixes para várias populações iniciais.
(e) Resolva essa equação diferencial explicitamente, usando frações parciais ou com um sistema de computação algébrica. Use as populações iniciais de e . Trace as soluções e compare com seus esboços na parte (d).
Passo 1
(a) E aê, pessoal! Aqui a gente tem uma equação diferencial que se parece bastante com a logística pra descrever uma população de peixes, mas tem um termo constante sendo subtraído. O que será que isso significa?
Bom, significa que há uma perda constante de peixes por semana (já que é medido em semanas). Nesse caso, pode ser que, por semana, peixes sejam pescados por humanos.
Passo 2
(b) Agora vamos desenhar um campo de direções que represente a equação diferencial:
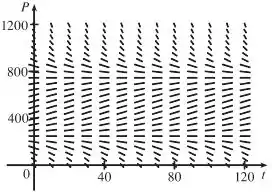
Passo 3
(c) As soluções de equilíbrio ocorrem quando a taxa de crescimento é nula, ou seja:
Resolvendo essa equação do grau, obtemos:
Então essas são as nossas soluções de equilíbrio!
Passo 4
(d) Agora vamos esboçar algumas soluções a partir do campo de direções:
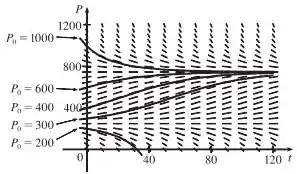
A gente já viu que existem duas soluções de equilíbrio aí. Mas repare que as demais soluções tendem a se afastar de , e tendem a se aproximar de , né mesmo?
Quem começa com uma população abaixo de tende a se extinguir, e acima disso, tende a se estabilizar em .
Passo 5
(e) Agora, com o auxílio de um sistema de computação algébrica, vamos resolver a equação diferencial do enunciado, com populações iniciais de e . (Dá pra fazer por frações parciais também, fique à vontade hahaha)
E agora a gente traça essas soluções:
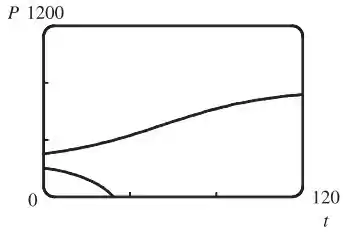
Repare que ficou bem parecido com o nosso esboço feito no item (d), para e .
Resposta
(c)
(e)