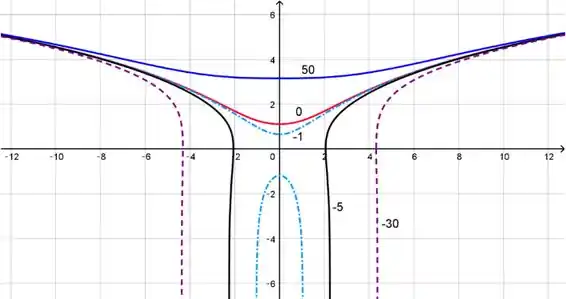
Resolva a equação e trace vários membros da família de soluções (se seu SCA fizer gráficos implícitos). Como muda a curva solução quando a constante C varia?

Como já separamos a equação, vamos integrar cada lado, né galera?

Vamos nos concentrar na primeira integral, que faremos por partes. Relembre-se:

Nesse caso, e

Agora olha pra segunda integral, uma substituição talvez resolve nosso problema, bora conferir?

A gente faz então . Substituindo na integral, fica assim:

Agora que temos os valores das integrais, vamos ver como nossa equação vai ficar:

Chegamos então a uma equação implícita, ou seja, não dá pra isolar o .

Agora vamos traçar algumas curvas da família de soluções, para acompanhar a evolução dos gráficos conforme a constante vai mudando.

Fazemos para os seguinte valores de