Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 3c
Resolva a inequação.
Passo 1
Para estudar o sinal da expressão vamos analisar o numerador e o denimonador separadamente:
Para temos:
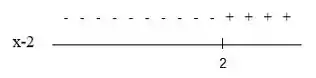
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
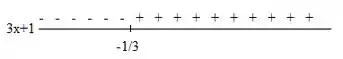
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 2
Vamos lá, para resolver a inequação vamos analisar as duas imagens que achamos no passo anterior:
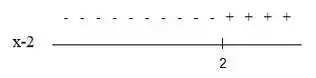
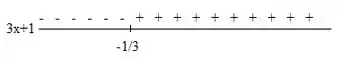
Temos que quando o numerador e o denominador tiverem sinais iguais, analisando as duas imagens vemos que isso acontece quando:
ou
Resposta
para ou
Exercícios de Livros Relacionados
Determinar todos os intervalos de um número que satisfaçam as desigualdades abaixo. Fazer a representação gráfica.m) x x - 34
Determinar todos os intervalos de um número que satisfaçam as desigualdades abaixo. Fazer a representação gráfica.p) x 3 - x 2 - x - 20
Demonstrar:Se xy , então x1 2 x + yy .
Determinar todos os intervalos de um número que satisfaçam as desigualdades abaixo. Fazer a representação gráfica.s) 8 x 3 - 4 x 2 - 2 x + 10
Determinar todos os intervalos de um número que satisfaçam as desigualdades abaixo. Fazer a representação gráfica.c) 2 - 3 - 3 x ≥ - 7