Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 17cd
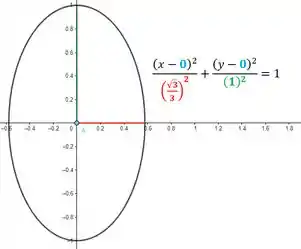
Para resolver os exercícios e , o aluno deve ter familiaridade com as equações diferenciais lineares de segunda ordem com coeficientes constantes.
Uma partícula partindo do ponto se move com vetor posição . Sabe-se que o vetor velocidade em cada instante é dado por .
c) Mostre que a curva descrita pela partícula é uma elipse
d) Qual o tempo necessário para que a partícula dê uma volta na elipse
Passo 1
Bora lá. Pra começar, vamos lembrar que:
Então do enunciado, tiramos:
Isso tá estranho né, mas da pra ajeitar! O próprio sistema de equações nos permite isso. Saca só essa manipulação doida:
Derivando:
Da segunda linha do sistema de equações:
E temos ainda, seguindo a mesma lógica:
Logo:
O que dá um sistema de EDO de 2ª ordem com a mesma cara tanto pra quanto pra , logo o mesmo tipo de solução. A equação característica, nos dois casos, é a mesma:
Eita! Raizes complexas na equação característica! Sendo assim a solução vai ter essa cara:
Onde:
Logo:
Passo 2
Agora falta determinar essas constantes, pra isso temos, do enunciado, o ponto inicial:
Logo:
Usando essas duas informações:
O que já adianta a gente na modelagem do vetor posição um pouco:
Agora essa é a parte que falamos do vetor velocidade. Apertem os sinto que vai começar a ficar cheio de letras. Como ele é a derivada da posição...
Seja, da igualdade dos vetores velocidade do enunciado e da definição:
Temos o seguinte sistema de equações:
O que, arrumando, dá:
Agora a gente pode eliminar o pra achar o . Pra isso, multiplicamos a primeira linha por :
E a segunda linha por :
Somando as duas equações, os termos de somem e ficamos com:
Logo, fechamos o componente do vetor posição:
E da seguinte igualdade, tirada lá do vetor velocidade:
Tiramos:
Show de bola, então terminamos de modelar o vetor posição. Note que se antes tínhamos:
O valor de então é . Usando a gente descobre isso mais rápido do que terminando de resolver o sistema. O vetor posição será:
Passo 3
Pra provarmos que isso é uma elipse, basta escrevermos as componentes da seguinte forma:
Assim galera, a gente consegue enxergar como manipular pra poder eliminar o parâmetro ; Bem, como os arcos dentro do seno e do cosseno são iguais, a gente pode tentar usar a propriedade trigonométrica:
Bora lá então:
E essa é a equação cartesiana de uma elipse centrada na origem , com semieixo na direção do eixo de tamanho e semieixo na direção do eixo de tamanho . O esboço seria:
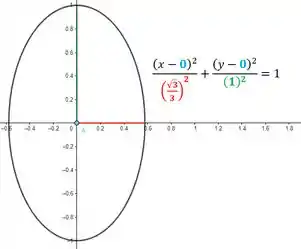
Resposta
