A respiração é cíclica, um ciclo completo respiratório que começa pela inalação e acaba pela expiração, durando cerca de 5 s. A taxa máxima do fluxo de ar para dentro dos pulmões é de cerca de 0,5 L/s. Isso explica, em parte, porque a função tem sido frequentemente usada para modelar a taxa de fluxo de ar para dentro dos pulmões. Use esse modelo para encontrar o volume de ar inalado nos pulmões no instante .

Opa, bora resolver essa questão!

Temos uma função que modela a taxa de fluxo de ar para dentro dos pulmões (lembre-se que quando temos taxa estamos falando de derivada!):

O problema também diz que a taxa máxima do fluxo de ar para dentro dos pulmões é de cerca de 0,5 L/s e o ciclo respiratório dura cerca de .

Sabendo disso tudo temos que encontrar o volume de ar inalado nos pulmões no instante .

Bom, vamos pensar um pouco aqui! O volume de ar inalado será dado em função do fluxo de ar que entra nos pulmões durante um determinado tempo.

Sendo assim, o volume total será a área abaixo da curva da função em um gráfico

E como a área abaixo da função é calculada?

Acertou quem disse por meio da integral!

Ok, mas como vamos resolver essa integral? Vamos aplicar substituição!

Então temos que identifique uma parte da função que, ao ser substituída, simplifique a integral. Vamos olhar a nossa integral:

Concorda comigo que só resolver uma integral de seno, é muito mais simples que resolver essa função composta, ?

Vamos chamar essa parte de , encontrar a derivada de em relação de , e isolar de .

Também vamos precisar trabalhar com os limites de integração. Queremos o ciclo respiratório dura cerca de , então nosso limite de integração irá de a , temos que calcular o valor de

Para ambos e assim poderemos montar a nossa integral!

Finalmente vamos integrar, para isso podemos usar uma tabela de primitivas:

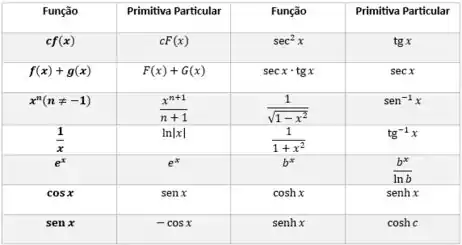
E por fim avaliar os limites de integração com o TFC (Teorema Fundamental do Cálculo), que nos diz que uma integral definita é a primitiva de função avaliada para o limite superior, menos a primitiva avaliada para a função inferior:

Ufa! Esse é nosso plano, eu sei que parece muita coisa, mas é mais simples do que parece!

Então mãos na massa!