Use o Exercício 92 para calcular a integral

Beleza??

Aqui temos que calcular a seguinte integral:

Usando o que foi feito no exercício 92.

Muito bem galera, quando vemos já podemos pensar logo naquela identidade trigonométrica:

Isolando o cosseno:

E já vamos substituir:

Temos agora uma função de seno:

Sendo assim:

Vamos relembrar o que foi feito no exercício 92?

Usamos uma técnica de integral por partes, vamos resumir aqui, quando temos algo do tipo:

Podemos passar a integral para o outro lado da integral (como se ela fosse uma varável:

E soma-las também como uma variável qualquer:

E assim temos o valor para 2 integrais, precisamos do valor de uma só, e como no caso dessa integral ser uma variável qualquer, só passamos o 2 para o outro lado dividindo:

Logo para esse caso temos:

E não para por aí! Vamos precisar usar a regra da substituição! Mas você lembrar o que ela fala?

Então temos que ela deve ser realmente o inverso da regra da cadeia. De acordo com a regra da cadeia para a derivada temos:

Na integração por substituição, pegamos uma expressão da forma e encontramos sua primitiva.

A integração por substituição nos ajuda a simplificar uma expressão confusa, transformando a função "interna" na variável. Então temos que encontrar o resultado dessa integral:

Para simplificar essa integral, colocamos uma nova variável tal que . Isso significa que .

Substituindo essas expressões na integral, obtemos:

A integral agora é muito mais simples de resolver, pois é uma função direta de . Após integrar em relação a , obtemos .

Finalmente, substituímos de volta por para obter a resposta na variável original .

Por fim vamos utilizar uma tabela de primitivas para nos ajudar na integração:

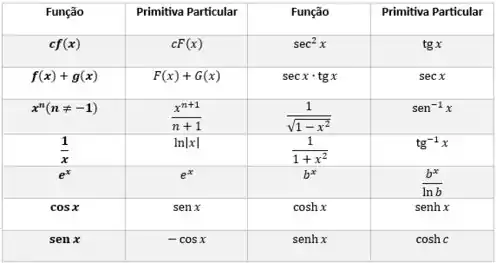
Eu sei o que você está pensando! Quanta coisa! Mas calma, no fim é mais simples do que parece!