Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.6 - Ex. 4b
Sabendo-se que o centro de massa de uma superfície é definido por
,e,
onde é a massa total de e é a densidade em cada ponto , calcule o centro de massa das seguintes superfícies com densidade constante.
b) é a parte da superfície cônica compreendida entre os planos e .
Passo 1
Bom galerinha, nós temos uma que está entre os planos e , uma vez que . Ou seja, o que queremos calcular é essa “partezinha” entre os planos e .
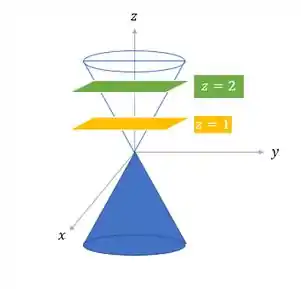
Passo 2
Nossas coordenas são:
Com os intervalos de integração:
Olhando, agora, só para o plano , temos que:
E
Passo 3
Agora, basta calcularmos o centro massa.
Resposta
Exercícios de Livros Relacionados
Calcule ∬ K f x , y , z d S sendo: f x , y , z = x y ;σ u , v = u - v , u +v ,2 u + v + 1 ,0 ≤ u ≤ 1e0 ≤ v ≤ u .
Calcule ∬ K f x , y , z d S sendo: d )f x , y , z = y ;σ u , v = u , v , 1 - u 2 ,0 ≤ u ≤ 1 ; 0 ≤ v ≤ u .
Calcule ∬ K f x , y , z d S sendo: d )f x , y , z = x 2 + y 2 ;σ a superfície x 2 + y 2 + z 2 = 4 ,z ≥ 1 . (Fica entendido aqui que σ é a parametrização mais “natural” do conjunto dado).
Calcule ∬ K f x , y , z d S sendo: g )f x , y , z = x ;σ é a parte da superfície z 2 = x 2 + y 2 situada entre os planos z = 1ez = 3 .
Calcule a massa da superfície σ dada, com função densidade superficial de massa f ( x , y , z ) dada: c )f x , y , z = 2 e σ u , v = u , v ,1 - u 2 ,0 ≤ u ≤ 1 ,0 ≤ v ≤ 1 .