Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.6 - Ex. 3

Seja S uma superfície fechada tal que S = S 1 ∪ S 2 , onde S 1 e S 2 são as superfícies de revolução obtidas pela rotação em torno do eixo z das curvas C 1 : z = 1 - x , 0 ≤ x ≤ 1   e C 2 : z = 0 , 0 ≤ x ≤ 1 , respectivamente. Se ρ x , y , z = x 2 + y 2 é a função que fornece a densidade (massa por unidade de área) em cada ponto x , y , z ϵ   S , calcule a massa de S .

Passo 1

Bom galera, nós temos que

C 1 : z = 1 - x ,   0 ≤ x ≤ 1

E

C 2 : z = 0 , 0 ≤ x ≤ 1

Nós temos a seguinte situação:

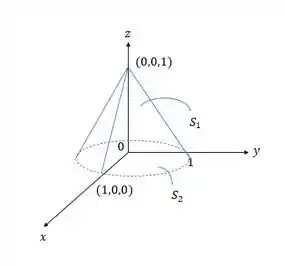
Passo 2

A sensidade é dada por:

ρ x , y , z = x 2 + y 2

S 1   c o n e : t , θ = ( t cos ⁡ θ , t   s e n   θ ,   1 - t )  

E o novo intervalo de integração é:

0 ≤ 1 - t ≤ 1

⇒ - 1 ≤ - t ≤ 0

Portanto 0 ≤ t ≤ 1 e 0 ≤ θ ≤ 2 π .

N t , θ = t ( cos ⁡ θ ,   s e n   θ ,   1 ) = ( t   c o s   θ ,   t   s e n   θ ,   t )

N ( t , θ ) = t 2 cos 2 ⁡ θ + t 2   s e n   θ + t 2 = 2 t 2 = t 2

Passo 3

Assim, já podemos montar nossa integral:

∬ S 1 x 2 + y 2   d S 1 = ∫ 0 2 π ∫ 0 1 t 2 cos 2 ⁡ θ + t 2   s e n 2 θ ⋅ t 2   d t   d θ = ∫ 0 2 π ∫ 0 1 t 2   2   d t   d θ = 2   ∫ 0 2 π t 3 3 0 1 d θ = 2 ⋅ 1 3 ⋅ 2 π = 2 2 π 3

Passo 4

S 1   c i r c u n f e r ê n c i a - d i s c o : r , θ = ( r cos ⁡ θ ,   r   s e n   θ ,   0 )

com o intervalo de integração de 0 ≤ θ ≤ 2 π e ≤ r ≤ 1 .

N r , θ = r 0,0 , - 1 = ( 0,0 , - r )

N ( r , θ ) = 0 + 0 + r 2 = r

Agora podemos montar nossa integral:

∬ S 2 x 2 + y 2 d S 2 = ∫ 0 2 π ∫ 0 1 r 2 cos 2 ⁡ θ + r 2 s e n 2   θ r d r d θ = ∫ 0 2 π ∫ 0 1 r 2 d r d θ = ∫ 0 2 π r 3 3 0 1 d θ = 1 3 ⋅ 2 π = 2 π 3

Passo 5

E então, para calcularmos a massa de S :

M = ∬ S 1 x 2 + y 2 d S 1 + ∬ S 1 x 2 + y 2 d S 2 = 2 2 π 3 + 2 π 3

M = 2 π 3 2 + 1

Resposta

M = 2 π 3 2 + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estabeleça uma fórmula para o cálculo da área da superfície x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 , onde a0 ,bb ,c0 são constantes dadas
Seja F : Ω ⊂ R 3 → R , Ω aberto, uma função de classe C 1 tal que ∂ F ∂ z ≠ 0 em Ω . Seja f : K → R , onde K é um compacto com fronteira de conteúdo nulo e interior não-vazio contido em Ω , tal que F
Mostre que Se S é uma superfície dada na forma explicita pela equação y = y(x,z) ∫ ∫ S fd S =∫ ∫ R fx , y x , z ,z1 + ∂ y ∂ x 2 + ∂ y ∂ z 2 d x d z Onde R é a projeção de S sobre o plano XZb) Se S é d
Dada a equação vetorial ru , v = u cos ⁡ v ,us e nv , u ² ² b) fazer esboço e indicar o significado geométrico dos parâmetros u e vc) determinar a área da parte da superfície que esta entre os planos
Considerando que a superfície S é obtida girando a curva z = x 2 , 0 ≤ x ≤ 4 , em torno do eixo z , pede-seUma parametrização para S .