Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.7 - Ex. 6
São mostrados os gráficos das funções posição de duas partículas, com medido em segundos. Quando cada partícula está acelerando? Quando está freando? Explique.
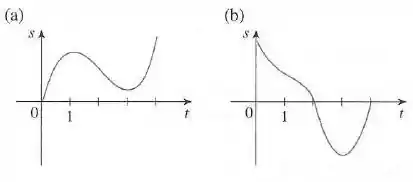
Passo 1
Opa, bora analisar os dois graficos
Os dois são gráficos da função velocidade de duas partículas com em segundos. Queremos saber quando cada partícula está acelerando e freando!
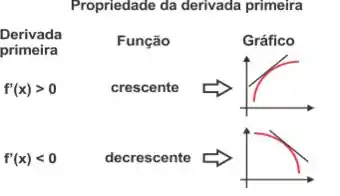
A aceleração é a derivada da velocidade, então a aceleração é positiva quando a reta tangente a curva tem inclinação positiva e freando quando a sua inclinação é negativa!
Passo 2
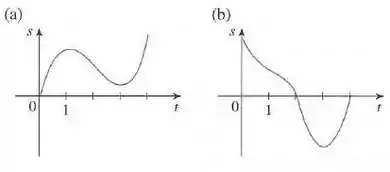
Para o gráfico a, temos a seguinte imagem:
Para a curva (a) avaliando graficamente:
- para
ii) para
Para a curva (b) avaliando graficamente:
- para
ii) para
Passo 3
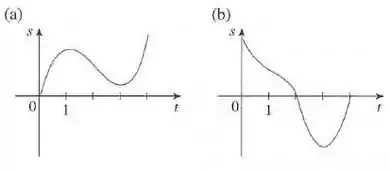
Se analisarmos o sinal da segunda derivada das curvas e utilizando as informações da imagem abaixo, temos que:
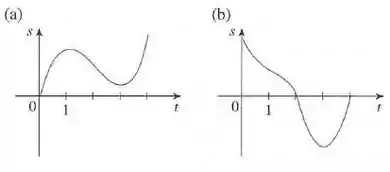
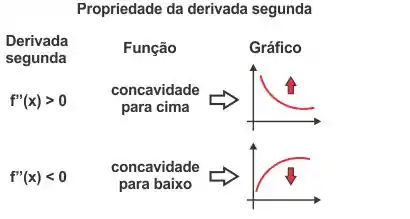
Para a curva (a) avaliando graficamente:
- para
ii) para
Para a curva (b) avaliando graficamente:
- para
ii) para
Passo 4
Agora, se cruzarmos as informações, podemos saber onde as partículas estão acelerando e onde estão freando, pois sabemos que quando e têm o mesmo sinal a partícula está acelerando e quando têm sinais opostos, ela está freando
Para (a). A partícula está acelerando nos intervalos
E está freando nos intervalos
Para (b). A partícula está acelerando no intervalo
E está freando no intervalo
Resposta
Para (a). A partícula está acelerando nos intervalos
E está freando nos intervalos
Para (b). A partícula está acelerando no intervalo
E está freando no intervalo