Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.1 - Ex. 21
Seja .
a) Esboce o gráfico de .
b) Determine e .
Passo 1
É dada uma função de duas variáveis e o precisamos esboçar o gráfico da , assim como obter suas derivadas.
Para esboçar o gráfico, devemos analisar um pouco o jeitão da , vendo seus valores para alguns pontos- por exemplo.
Já para determinar as derivadas, basta derivar a função em duas situações:
-para a região onde
-para a região onde
Passo 2
Pela equação da , vemos que ela é zero para todos os pontos fora do círculo de raio 1 centrado na origem. Já dentro desse círculo, ela tem um comportamento exponencial.
De fato, para , temos .
Para temos . Ou seja, a função começa em nas bordas do círculo de raio 1 e termina no valor , como se a fosse um chapéu ou algo assim.
A partir do que observamos, já podemos esboçar um gráfico aproximado:
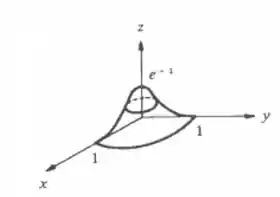
Passo 3
Agora, para saber as derivadas da , basta olhar o que que acontece nas duas regiões nas quais está definida.
Para , temos toda vida. Ou seja, suas derivadas também são nulas:
para
Já na outra região, temos
Ou seja
Analogamente, vamos obter
Resposta
a)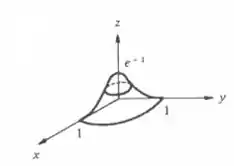
b) para
para