Seja
- Seja a curva obtida como intersecção da superfície de equação com o plano . Calcule
Especificando a orientação escolhida.
Passo 1
Seguindo nessa questãozinha. Vimos na letra A que sim! O campo é conservativo.
Agora vamos ter que procurar pela função ; lembrando que:
Mas aaaantes disso, tava quase esquecendo né?! Precisamos esboçar as superfícies e tentar encontrar a intersecção:
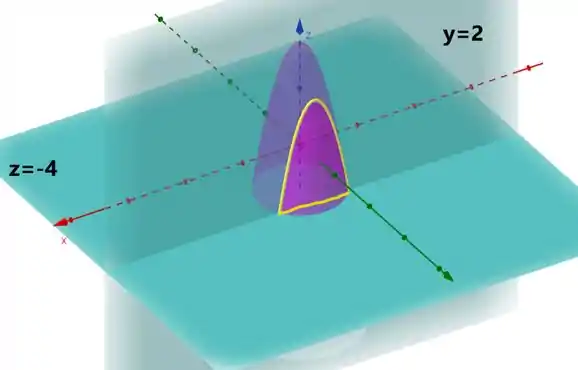
A intersecção é aquela curva em amarelo na imagem. Vamos isolar ela, para ficar menos poluído esse negócio.
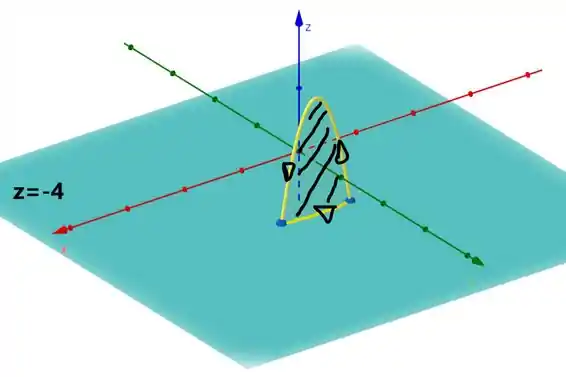
De quebra já deixei claro ali a orientação para a curva (anti-horário).
Passo 2
Bom, porque a gente precisou desenhar isso? Bom lembra que a gente disse que o campo era conservativo??
Ou seja, só importa os pontos de saída e de chegada. Então, devemos escolher dois pontos sob a curva em amarelo para poder calcular a integral.
Vamos fazer isso com base na intersecção, então adotando e :
Portanto:
Ou seja, teremos os seguinte pontos:
Perfeito. Lembra que:
Onde o nosso campo (não! Não é o programa) é definido assim:
Então agora só precisamos obter esse para enfim obter a resposta do exercício.
Bom, lembra que na letra A concluímos que esse é definido assim:
Então vamos abrir essa expressão:
E
Passo 3
Ta comigo? Vamos integrar qualquer uma daquelas expressões para tentar achar o :
Teremos:
Peraí? Da onde saiu aquele ali?? Seguinte, estamos simplesmente admitindo que possa existir uma função que não seja dependente de . Porque se ela não é dependente de a hora que derivamos ela é considerada uma constante e então desaparece.
Vamos então assumir que aquela expressão seja verdadeira; se derivarmos ela em função de esperamos obter .
Isso tem que ser igual a , então:
A única forma de isso ser verdade é se:
E então:
Encontramos:
Novamente, estamos admitindo a possibilidade de existir algo em função de ; no final das contas a nossa função tem a seguinte cara, até agora:
Agora, se derivamos isso em , vamos querer achar a função .
Huuuummm interessante, então a única possibilidade:
Integrando isso:
Obtemos:
Então no final de todo esse rolê, obtemos a seguinte forma para a função :
Ufa! Deu pra suar um bocado! Mas falta terminar o bang
Então:
Conseguimos encontrar esses aê lembrando que os nossos pontos são: .
E
Portanto:
Acho que é isso!! Haahhahaha
Até a próxima!
Resposta
Só concluindo,