Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.5 - Ex. 4

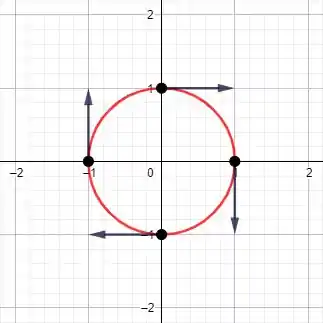
Seja f x , y = arctg ⁡ x y . Represente geometricamente ∇ f x 0 , y 0 , sendo x 0 , y 0 um ponto da circunferência x 2 + y 2 = 1 .

Passo 1

O gradiente de f é definido como

∇ f x , y = f x x , y , f y x , y

Calculando as derivadas

f x x , y = 1 1 + x y 2 1 y = 1 1 + x 2 y

= 1 x 2 + y 2 y = y x 2 + y 2

f y x , y = 1 1 + x y 2 - x y 2

= - x x 2 + y 2

Então temos o gradiente

∇ f x , y = y x 2 + y 2 , - x x 2 + y 2

No ponto x 0 , y 0

∇ f x 0 , y 0 = y 0 x 0 2 + y 0 2 , - x 0 x 0 2 + y 0 2

Passo 2

Pegando alguns pontos dentro da circunferência x 2 + y 2 = 1 :

No ponto x 0 , y 0 = 1,0

∇ f 1,0 = 0 , - 1

No ponto x 0 , y 0 = 0,1

∇ f 0,1 = 1,0

No ponto x 0 , y 0 = - 1,0

∇ f 0,1 = 0,1

No ponto x 0 , y 0 = 0 , - 1

∇ f 0,1 = - 1,0

Passo 3

Jogando esses pontos e vetores no plano temos

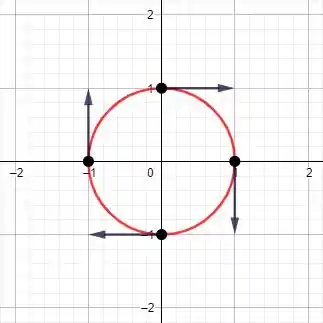
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o vetor gradiente das funções dadas nos pontos indicados:i) f x ,t = x + 2 t ln ⁡ ( x + 2 t ) ; P e , 1
Determinar o vetor gradiente das funções dadas nos pontos indicados:b) z = x 2 y + 3 x y + y 2 ; P 0 ,3
Determinar o vetor gradiente das funções dadas nos pontos indicados:g) f u ,v ,w = u 2 + v 2 - w 2 + u v w ; P 0,1 ,0
Determinar o vetor gradiente das funções dadas nos pontos indicados:c) z = s e n( 3 x + y ) ; P 0 , π 2
Determinar o vetor gradiente das funções dadas nos pontos indicados:f) z = x y - s e n( x + y ) ; P π 2 , 0