Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.1 - Ex. 26

  1. Seja A n a área de um polígono com lados iguais inscrito num círculo com raio r. Dividindo o polígono em triângulos congruentes com ângulo central de 2 π n , mostre que:

    2. A n = 1 2 n r ² . s e n   2 π n

  2. Mostre que lim n → ∞ ⁡ A n = π r ² . [Dica: Use a Equação 3.3.2.]

Passo 1

Bom galera, vamos começar desenhando o triângulos congruentes com ângulo central de 2 π n que fazem parte do polígono circunscrito no círculo de raio r:

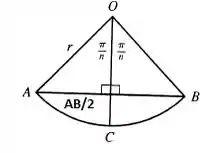
Reparem que temos um triângulo isósceles com dois lados iguais a r. Se desenharmos um terceiro raio, atuando como a bissetriz do triângulo, vamos dividir o ângulo e o lado AB pela metade ( π n ), formando dois triângulos retângulos, como no desenho!

Bom, queremos a área do triângulo retângulo para conseguir a área do triângulo maior. E como calculamos a área do triângulo?

A = B a s e × A l t u r a 2

E temos que relacionar com o ângulo, então vamos o seno e cosseno. O seno é dado por:

s e n   π n = C O H

E o cosseno é dado por:

cos ⁡ π n = C A H

Passo 2

Usando as definições de seno e cosseno temos:

s e n   π n = C O H

O cateto oposto é a base, certo?

s e n   π n = B a s e r

B a s e = r s e n   π n

Vamos para o cosseno:

c o s   π n = C A H

Já o cateto adjacente representa a altura:

cos ⁡ π n = A l t u r a r

A l t u r a = r . cos ⁡ π n

Vamos jogar na área:

A = r s e n   π n × r . cos ⁡ π n 2

A = r ² s e n   π n . cos ⁡ π n 2

Se esta é a área de um triângulo retângulo, a área do triângulo total é o dobro, correto?

A A o B = 2 . r 2 s e n   π n . cos ⁡ π n 2

A A o B = r ² s e n   π n . cos ⁡ π n

Lembrando da identidade:

1 2 s e n   2 π n = s e n   π n . cos ⁡ π n

Então a área:

A A o B = 1 2 r 2 s e n   2 π n

Para os n triângulos formadores do polígono:

A n = 1 2 n r 2 s e n   2 π n

Passo 3

Na letra b vamos calcular o lim n → ∞ ⁡ A n .

E para isso nós vamos ter que usar a Equação:

l i m θ → 0 s e n   θ θ = 1

Então para a área:

A n = 1 2 n r 2 s e n   2 π n

Nós teremos que fazer aparecer no denominador o termo 2 π n . Para facilitar vamos chamar:

θ = 2 π n → n = 2 π θ

Quando n → ∞ , nosso θ tenderá a zero, não é? Então substituindo:

l i m θ → 0 1 2 . 2 π θ . r 2 s e n   θ = l i m θ → 0 π r 2 s e n   θ θ

As constantes podem sair do limite:

= π r 2 l i m θ → 0 s e n   θ θ

Usando a equação dada acima:

= π r 2 . 1

Concluindo:

lim n → ∞ ⁡ A n = π r 2

Resposta

Demonstração nos Passos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Estime a área sob o gráfico de f x = 1 + x ² ²de x = - 1 até x = 2 usando três retângulos aproximantes e extremidades direitas. Então, aperfeiçoe sua estimativa utilizando seis retângulos aproxima
(a) Lendo os valores do gráfico dado de f , utilize cinco retângulos para encontrar as estimativas inferior e superior para a área sob o gráfico dado de f de x = 0 até x = 10 . Em cada caso, esboce os
Óleo vaza de um tanque a uma taxa de r t litros por hora. A taxa decresce à medida que o tempo passa e os valores da taxa em intervalos de duas horas são mostrados na tabela a seguir. Encontre estimat
A velocidade de um corredor aumenta regularmente durante os três primeiros segundos de uma corrida. Sua velocidade em intervalos de meio segundo é dada em uma tabela. Ache as estimativas superior e in
O gráfico da velocidade de um carro em aceleração a partir do repouso até uma velocidade de 120k m / h em um período de 30 segundos é mostrado. Estime a distância percorrida durante esse período.