Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 1

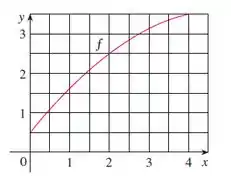
Seja I = ∫ 0 4 f x d x , em que f é a função cujo gráfico é mostrado.

  1. Use o gráfico para encontrar L 2 , R 2 e M 2 .
  2. Estas são estimativas por baixou ou por cima de I ?
  3. Use o gráfico para achar T 2 . Como isso se compara com I ?
  4. Para qualquer valor de n , liste os números L n , R n , M n , T n e I na ordem crescente.

Passo 1

  1. Temos o intervalo 0 ≤ t ≤ 4 , e vamos usar n = 2 , temos que ∆ x :

    2. ∆ x = b - a n = 4 - 0 2 = 2

    Primeiro vamos achar a aproximação a esquerda L 2 , onde os x dos pontos são o ponto a esquerda em cada intervalo:

    L 2 = ∑ i = 1 n f x i - 1 ∆ x = f x 0 + f x 1 2 = f 0 + f 2 2 = 0,5 + 2,5 2 = 6

    Passo 2

    Agora vamos achar a aproximação a direita R 2 , onde os x dos pontos são o ponto a direita em cada intervalo:

    R 2 = ∑ i = 1 n f x i ∆ x = f x 1 + f x 2 2 = f 2 + f 4 2 = 2,5 + 3,5 2 = 12

    Passo 3

    Agora vamos achar a aproximação do ponto médio M 2 , onde os x dos pontos são os pontos médios de cada intervalo:

    M 2 = ∑ i = 1 n f x i - ∆ x = f x 1 - + f x 2 - 2 = f 1 + f 3 2 = 1,6 + 3,2 2 ≈ 9,6

    Passo 4

  2. L 2 é subestimado, uma vez que a área sob os pequenos retângulos é menor que a área sob a curva. R 2 é superestimado, uma vez que a área sob os retângulos grandes é maior que a área sob a curva. E M 2 parece ser superestimado também, embora seja bastante próxima de I .

    3. Passo 5

  3. Para achar a aproximação pela Regra do Trapézio temos a fórmula:

    4. T 2 = 1 2 ∆ x f x 0 + 2 f x 1 + f x 2 = 1 2 ∙ 2 f 0 + 2 f 2 + f 4 = f 0 + 2 f 2 + f 4 = 0,5 + 2.2,5 + 3,5 = 9

    Essa aproximação é subestimada, já que o gráfico é côncavo para baixo.

    Passo 6

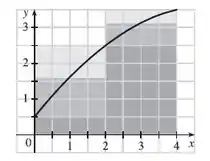
  4. Para qualquer n observado no gráfico abaixo, nós vamos ter que as aproximações a esquerda e do trapézio são menores que I e as do ponto médio e da direita são maiores:

L n < T n < I < M n < R n

Resposta

  1. L 2 = 6 , R 2 = 12 e M 2 ≈ 9,6
  2. L 2 é subestimado, R 2 e M 2 são superestimados
  3. T 2 = 9 , e T 2 é superestimado
  4. L n < T n < I < M n < R n
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O gráfico de y = 4 - | x | e o eixo x de x = - 4 até x = 4 formam um triângulo. Use o método desta secção para encontrar sua área.
Nos exercícios de 39 a 44, ache a área da região, tomando como medida da altura do i - é s i m o é retângulof ( m i ) , onde m i é o ponto médio do i - é s i m o é subintervalo. Sugestão: m i = 1 2 x
Nos exercícios de 39 a 44, ache a área da região, tomando como medida da altura do i - é s i m o é retângulof ( m i ) , onde m i é o ponto médio do i - é s i m o é subintervalo. Sugestão: m i = 1 2 x
Nos exercícios de 39 a 44, ache a área da região, tomando como medida da altura do i - é s i m o é retângulof ( m i ) , onde m i é o ponto médio do i - é s i m o é subintervalo. Sugestão: m i = 1 2 x
Use o método desta secção para encontrar a área de um trapézio isósceles cujas bases têm medidas b 1 e b 2 e cuja altura tem medida h .