Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.1 - Ex. 4

Seja K o triangulo a seguir e γ a fronteira de K orientada no sentido anti-horário. Sejam P ( x ,   y ) e Q ( x ,   y ) de classe C 1 num aberto contendo K .

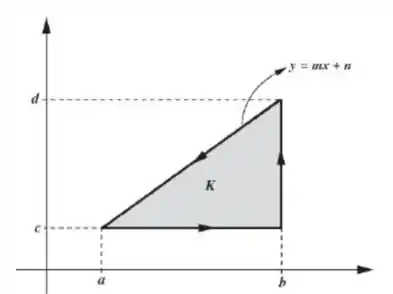
Prove que

∮ γ P d x + Q d y = ∫ ∫ K ∂ Q d x - ∂ P ∂ y d x d y

(Sugestão: Prove que ∮ γ P d x = - ∫ ∫ K ∂ P ∂ y d x d y e ∮ γ Q d y = ∫ ∫ K ∂ Q ∂ x d x d y

Passo 1

Nesse problema vamos calcular as integrais de cada lado da igualdade, identificando cada γ para as curvas e aplicando as propriedades das integrais. Quando calcularmos de cada lado da igualdade vamos ver que são equivalentes, provando, assim, o que foi pedido no enunciado. Vamos lá!

Passo 2

Bem, vamos primeiro reescrever nossa integral. Dissemos no passo 1 que para provar essa igualdade precisamos calcular os dois lados da igualdade. Vamos então calcular o lado da esquerda primeiro.

∮ γ P x , y d x = ∫ γ 1 P x , y d x + ∫ γ 2 P x , y d x - ∫ γ 3 P x , y d x

O sinal negativo na ultima integral é dado por estar voltando o trajeto. Pra calcular essas equações, precisamos antes encontrar quem são nossos γ . Vamos observar nossa figura e definir quem são:

γ 1 : x = t y = c       d x = d t ,     a ≤ t ≤ b

γ 2 : x = b y = t       d x = 0 ,     a ≤ t ≤ b

γ 3 : x = t y = m t + n       d x = d t ,     a ≤ t ≤ b

Assim, temos que nossa integral fica:

∮ γ P x , y d x = ∫ a b P t , c d t - ∫ a b P t , m t + n d t

Se calcularmos agora o outro lado da integral, teremos que:

- ∫ ∫ K ∂ P ∂ y d x d y = - ∫ a b ∫ c m x + n ∂ P ∂ y d y d x = - ∫ a b P x ,   m x + n - P x ,   c d x =

= ∫ a b P x ,   c - P x ,   m x + n d x

Que, ainda bem, são equivalentes, mostando que ∮ γ P d x = - ∫ ∫ K ∂ P ∂ y d x d y .

Passo 3

De modo semelhante, porém agora para Q , teremos que:

∮ γ Q x , y d y = ∫ γ 1 Q x , y d y + ∫ γ 2 Q x , y d y - ∫ γ 3 Q x , y d y

Encontrando os γ , vamos ter que:

γ 1 : x = t y = c       d y = 0 ,     c ≤ t ≤ d

γ 2 : x = b y = t       d y = d t ,     c ≤ t ≤ d

γ 3 : x = t - n m y = t       d y = d t ,     c ≤ t ≤ d

Substituindo, vamos ter que:

∮ γ Q x , y d y = ∫ c d Q b , t d t - ∫ c d Q t - n m , t d t

Calculando agora o outro lado da igualdade, vamos ter que:

∫ ∫ K ∂ Q ∂ x d x d y = ∫ c d ∫ t - n m b ∂ Q ∂ x d x d y = ∫ c d Q b ,   t - Q t - n m ,   t d y

Mostrando também que é igual. Como podemos escrever

∮ γ P d x + Q d y = ∮ γ P d x + ∮ γ Q d y

temos também que

∮ γ P d x + Q d y = ∫ ∫ K ∂ Q d x - ∂ P ∂ y d x d y

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C sen ⁡ y d x + x cos ⁡ y d y C é a elipse x 2 + x y + y 2 = 1
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos ⁡ y 2 d y C é a fronteira da região englobada pelas parábolas y = x
Utilize o teorema de Green para encontrar a circulação anti-horária e o fluxo exterior para os campos e curvas nos Exercícios 49 e 50.Triângulo F = y - 6 x 2 i + x + y 2 j . C: O triângulo formado pel
Integral de linha nula – Mostre que ∮ ln ⁡ x sen ⁡ yd y - cos ⁡ y x d x = 0 para qualquer curva fechada C à qual o teorema de Green se aplica.
Utilize o teorema de Green para encontrar a circulação anti-horária e o fluxo exterior para os campos e curvas nos Exercícios 49 e 50.49. Quadrado F = 2 x y + x i + x y - y j C: O quadrado limitado po