Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.1 - Ex. 8

(Teorema de Green para um círculo.) Seja B o círculo de centro na origem e raio r . Seja γ t = r cos ⁡ t , r   s e n   t , 0 ≤ t ≤ 2 π . Suponha que P e Q sejam de classe C 1 num aberto Ω contendo B . Prove

∮ γ P d x + Q d y = ∬ B ∂ Q ∂ x - ∂ P ∂ y d x d y

Passo 1

Primeiro vamos apresentar nosso conjunto

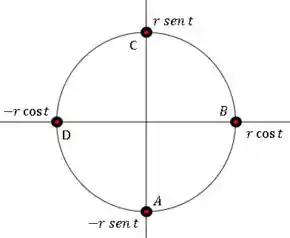
Assim talvez fique mais fácil de resolver nosso problema

Assim vamos tentar mostrar a relação entre

∫ γ P d x = - ∬ K ∂ P ∂ y d y d x

e

∫ γ Q d y = ∬ K ∂ Q ∂ x d x d y

Passo 2

Vamos primeiro mostrar nossa relação para

∫ γ P d x = - ∬ K ∂ P ∂ y d y d x

O termo da esquerda fazemos de forma simples. Tome como foi dado que γ t = r cos ⁡ t ,   r   s e n   t com t ∈ 0,2 π .

Assim temos

∫ 0 2 π P r cos ⁡ t , r   s e n   t - r   s e n   t d t

Agora o termo da direita

- ∬ K ∂ P ∂ y d y d x = - ∫ - r r ∫ - r 2 - x 2 r 2 - x 2 ∂ P ∂ y d y d x

Que pelo teorema fundamental do calculo é

- ∫ - r r P x , r 2 - x 2 - P x , - r 2 - x 2 d x

Tomando que x = r cos ⁡ t

Ficamos com

- ∫ 0 π P r cos ⁡ t , r   s e n   t - P r cos ⁡ t , - r   s e n   t - r   s e n   t d t

Na qual nosso limite de - r , r → [ 0 , π ]

Agora repare que o segundo termo temos como parametrização γ 1 t = r cos ⁡ t , - r   s e n   t , tal que γ t = - γ 1 t

Agora

∫ 0 π 2   P r cos ⁡ t ,   r   s e n   t r   s e n   t d t

Agora colocamdo o 2 em nosso limite de integração, dessa forma

∫ 0 2 π P r cos ⁡ t , r   s e n   t r   s e n   t

Assim conseguimos mostrar que

∫ γ P d x = - ∬ K ∂ P ∂ y d y d x

Passo 3

Agora vamos mostrar que

∫ γ Q d y = ∬ K ∂ Q ∂ x d x d y

Assim como em P , tome y = r   s e n   t → d y = r cos ⁡ t   d t

Logo

∫ γ Q d y = ∫ 0 2 π Q r cos ⁡ t , r   s e n   t r cos ⁡ t d t

Agora para a integral dupla

∬ K ∂ Q ∂ x d x d y = ∫ - r r ∫ - r 2 - y 2 r 2 - y 2 ∂ Q ∂ x d x d y

E novamente usando teorema fundamental do calculo

∫ - r r Q r 2 - y 2 , y - Q - r 2 - y 2 , y d y

E como y = r   s e n   t , temos - r , r → π 2 , 3 π 2 , ou seja

∫ π / 2 3 π / 2 Q r cos ⁡ t , r   s e n   t - Q - r cos ⁡ t , r   s e n   t r cos ⁡ t d t

Onde novamente tomando γ 2 t = - r cos ⁡ t ,   r   s e n   t , temos que γ t = - γ 2 t

Assim temos

∫ π / 2 3 π / 2 2 Q r cos ⁡ t ,   r   s e n   t r cos ⁡ t d t

E agora seguindo a mesma lógica

∫ π 3 π Q r cos ⁡ t , r   s e n   t r cos ⁡ t d t = ∫ 0 2 π Q r cos ⁡ t , r   s e n   t r cos ⁡ t d t

Mostrando que

∫ γ Q d y = ∬ K ∂ Q ∂ x d x d y

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C.F = (y2 – x2)i + (x2 + y2)jC: O triângulo limitado por
Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = ( x + 3 y ) i + ( 2 x - y ) j
Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = t g - 1 ⁡ y x i + l n ⁡ x 2 + y 2 j C : A frontei
Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circula-ção em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = ( x - y ) i + ( y - x ) j C : O quadrado limitad
O que é o teorema de Green? Como se pode interpretá-lo?