Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 10.2 - Ex. 6

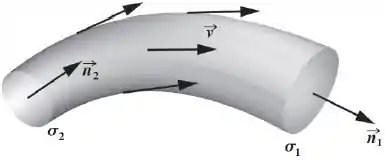
6. Seja v → um campo vetorial de classe C1 no aberto Ω e tal que div v → = 0 em Ω. Seja B ⊂ Ω um compacto em forma de “tubo” (veja figura) ao qual o teorema da divergência se aplica. Sejam σ 1 e σ2 as secções transversais, com normais n 1   → apontando para fora n 2   e apontando para dentro de B. Suponha que v →   seja tangente à superfície lateral do tubo.

∫ ∫ σ 2 v → ⋅ n 2 →   d S = ∫ ∫ σ 1 v → ⋅ n 1 →   d S  

Passo 1

Aqui vamos ter usar de logica e da equação de continuidade para resolver. Temos essa equação que nos diz

d ρ d t + ∇   .   p v = 0  

Essa é Equação da continuidade. Que diz que que a variação da densidade do fluido pelo tempo é causado por alguma Fonte ou Sumidouro Vetorial.

O enunciado diz que ∇   .   v = 0 , logo como a densidade é um escalar, não altera o produto vetorial que é divergente. Logo ∇   .   p v = 0 que implica em

d ρ d t = 0  

OU seja dentro da nossa superfície fechada não há variação de densidade do fluido. Então basicamente “O que entra sai”.

Passo 2

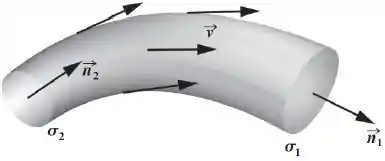
Quando temos esse tubo fechado e sabemos que “o que entra sai” , logo o fluxo que atravessa σ 2   obrigatoriamente tem que atravessar σ 1 e assim

∫ ∫ σ 2 v → ⋅ n 2 →   d S = ∫ ∫ σ 1 v → ⋅ n 1 →   d S  

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja F um campo cujas componentes têm derivadas parciais de primeira ordem contínuas em uma parte do espaço contendo uma região D delimitada por uma superfície fechada e lisa S. se │ F │ ≤ 1 ,│ │ pode
A base da superficie fechada de tipo cubico mostrada aqui e o quadrado unitario no plano xy. Os quatro lados estao nos planos x = 0, x = 1, y = 0 e y = 1. O topo e uma superficie lisa arbitraria cuja
a) Mostre que o fluxo exterior do campo vetorial de posicao F = xi + yj + zk atraves de uma superficie S fechada e lisa e tres vezes o volume da regiao delimitada pela superficie.b) Seja n o campo vet
Se f = M i + N j + P k é um campo vetorial diferenciável, definimos a notação f . ∇ para significar M ∂ ∂ x + N ∂ ∂ y + P ∂ ∂ z . Para campos vetoriais difernciáveis f 1ef 2 , verifique as identidades
Dentre todos os solidos retangulares definidos pelas desigualdades 0 ≤ x ≤ a ,0 ≤ y ≤ b ,0 ≤ z ≤ 1 , encontre aquele para o qual o fluxo exterior total de F = - x 2 - 4 x y i - 6 y z j + 12 z k atrave