Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 7

7. Seja σ a superfície e sejaum campo vetorial de classe C1 num aberto contendo σ. Justifique aafirmação

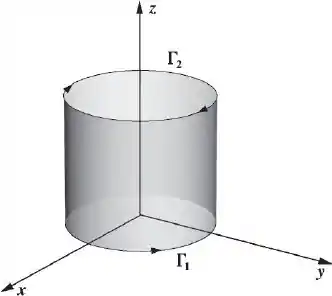
onde Γ1 (t) = (cos t, sen t, 0), 0 ≤ t ≤ 2π, Γ2 (t) = (cos t, - sen t, 1), 0 ≤ t ≤ 2π, e a normal apontando para fora do cilindro.

(Sugestão: Aplique o teorema de Stokes às porções de superfíciesregulares σ1 (u, v) = (cos u, sen u, v), 0 ≤ u ≤ π, 0 ≤ v ≤ 1, e σ2 (u, v) =(cos u, sen u, v), π ≤ u ≤ 2π, 0 ≤ v ≤ 1.)

Passo 1

Essa questão vai ser totalmente teórica, e vamos precisar usar de truques geométricos para sua resolução.

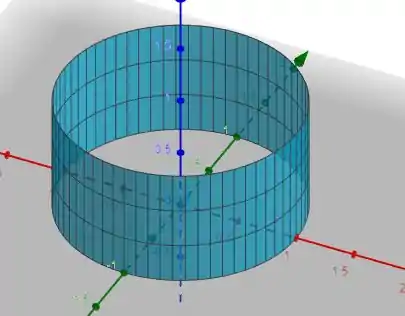
Temos essa casca cilíndrica. Para prova a proposição do enunciado precisaremos fazer o seguinte, partir essa casca em 2 partes.

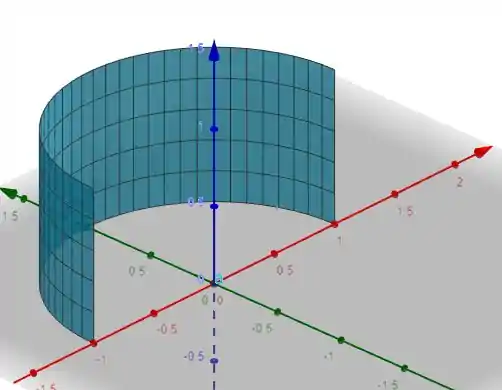
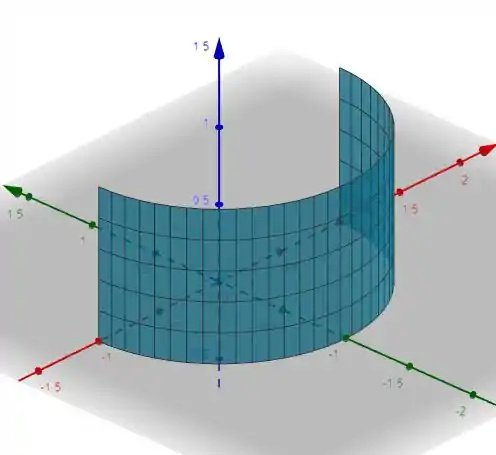
E vamos aplicar a integral de linha no contorno. Lembrando que sempre queremos o sentido anti-horario na nossa circulação. Assim os contornos ficam

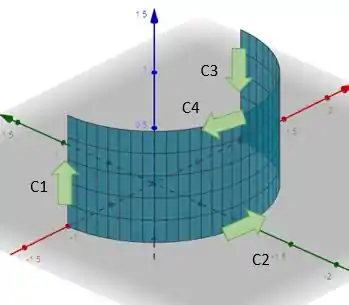
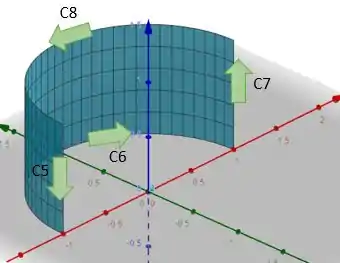
E faremos

Para todas as 8 curvas sinalizadas. Para economizar tempo podemos usar de logica. Afinal as curvas C5 e C1 são a mesma região, contudo estão em sentidos contrários, logo se somarmos as integrais de linha obtermos um valor nulo, pois elas se anularão. O mesmo raciocínio vale para as curvas C3 e C7. Logo Nossas integrais de linha se resumem a

Que são círculos em circulação contraria

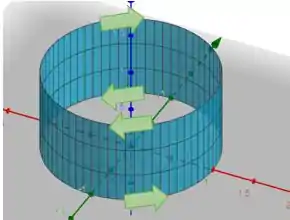
Passo 2

Podemos dizer então que C6 e C2 agora fazem parte da mesma curva, digamos .

E também que C4 e C8 estão também na mesma curva, digamos .

Logo uma possível parametrização poderia ser

E com isso conseguimos provar o teorema do enunciado.Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = x + y 2 i → + y + z 2 j → + ( z + x 2 ) k → , C o triâ

Use o Teorema de Stokes para calcular ∫ C F → ⋅ d r → , onde F → x , y , z = x 2 y i → + x 3 3 j → + x y k → e C é a curva da intersecção do paraboloide hiperbólico z = y 2 - x 2 com o cilindro x 2 +

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k

Suponha que S e C satisfaçam as hipóteses do Teorema de Stokes, e feg tenham derivadas parciais de segunda ordem contínuas. Use os exercícios 24e26 da seção 16.5 para demonstrar o seguinte: ∫ C f ∇ g

Calcule ∫ C y + s e n x d x + z 2 + c o s y d y + x 3 d z Onde C é a curva r → t = s e n t ,c o s t ,2 t , 0 ≤ t ≤ 2 π . (Sugestão: observe que C está na superfície z = 2 x y )