Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.3 - Ex. 2-a

2. Seja B um compacto com fronteira de conteúdo nulo e com interior nãovazio e seja δ (x, y) contínua em B. Seja α ≠ 0 um real dado. Considere amudança de coordenadas

x , y = s u + t v

Onde

u = cos ⁡ α i + sin ⁡ α   j

v =   - sin ⁡ α   i + cos ⁡ α j

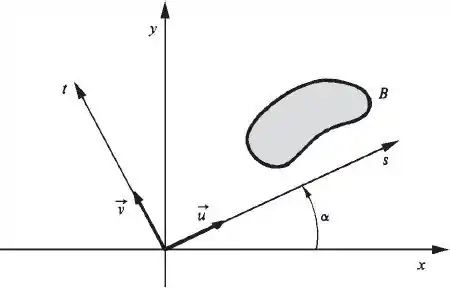
Bxy é o conjunto B olhado em relação ao sistema xy e Bst é o conjunto Bolhado em relação ao sistema st. Observe que Bxy é a imagem de Bstpela mudança de coordenadas acima.

a. Verifique que

x = s cos ⁡ α - t s i n   α

y = s sin ⁡ α + t cos ⁡ α  

E conclua que

∂ x , y ∂ s , t = 1

Passo 1

Para verificar que

x = s cos ⁡ α - t s i n   α

y = s sin ⁡ α + t cos ⁡ α  

Basta olhar para o enunciado que diz

x , y = s u + t v

Onde

u = cos ⁡ α i + sin ⁡ α   j

v =   - sin ⁡ α   i + cos ⁡ α j

São duas formas de escrever a mesma coisa. Podemos ainda escrever na forma matricial

x y =   cos ⁡ α - sin ⁡ α sin ⁡ α cos ⁡ α s t

Todas essas formas dizem a mesma coisa, temos so que nos acostumar com elas, ou escolher uma que nos seja mais fácil de compreender. Particularmente , a forma matricial é um modo mais elegante de escrever Rotação de Eixos.

Passo 2

Concluir que

∂ x , y ∂ s , t = 1

Significa dizer que o jacobiano dessa rotação é 1. Ou seja não deformamos o espaço, nem nossos objetos, ao mudar de variável. Estamos apenas olhando para o espaço amostral de maneira diferente. Podemos provar isso fazendo o determinante de

cos ⁡ α - sin ⁡ α sin ⁡ α cos ⁡ α

Que nos da

J = cos 2 ⁡ α +   sin 2 ⁡ α = 1

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .2-
Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .1
Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .
Calcule a integral iterada, convertendo-a antes para coordenadas polares. ∫ 0 2 ∫ - 4 - y 2 4 - y 2 x 2 y 2d x d y
Utilize a integral dupla para determinar a área da região.20- A região dentro do círculo r = 4s e nθ e fora do círculo r = 2