Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 5
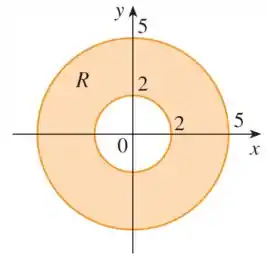
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma arbitrária qualquer contínua em .
Passo 1
Faala, galera!
Essa questão pede pra gente decidir que vamos usar coordenadas polares ou retangulares em uma região que ela dá, e transformar a integral
Em integral iterada.
Bom, nós usamos coordenadas polares quando temos uma região circular, de forma que a coordenada é a distância de um ponto dessa região até a origem (equivalente ao raio), e é referente a angulação partindo do eixo positivo de no sentido anti-horário. É isso aqui:
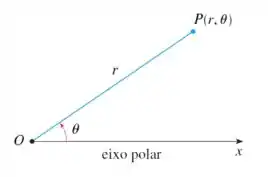
Pra fazer a mudança de coordenadas, usamos:
E para um círculo de raio , temos:
Como fazemos uma mudança de variáveis, temos que multiplicar o jacobiano no integrando. No caso de polares,
Então vamos olhar pra nossa região e entender se é uma região circular. Se for, vamos descrever com essas coordenadas.
Passo 2
Nossa região é essa aqui:
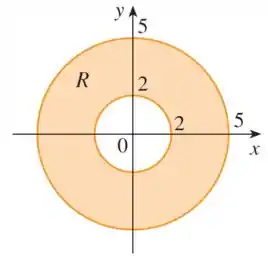
Percebe que é a região entre duas circunferências. Ou seja, é uma região circular!
Dessa forma, vamos usar coordenadas polares:
A integral vai ficar:
Passo 3
Só falta acharmos os limites de integração.
Como a região preenche todo o entorno do centro (não temos só uma seção circular), não temos restrições pra :
Já o , a nossa região tem um mínimo de , quando está no limite “interno”, que é a circunferência de raio , e máximo de , quando está no outro limite, que é a circunferência de raio :
Assim,
Resposta
Coordenadas polares.