Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.3 - Ex. 2-b

2. Seja B um compacto com fronteira de conteúdo nulo e com interior nãovazio e seja δ (x, y) contínua em B. Seja α ≠ 0 um real dado. Considere amudança de coordenadas

Onde

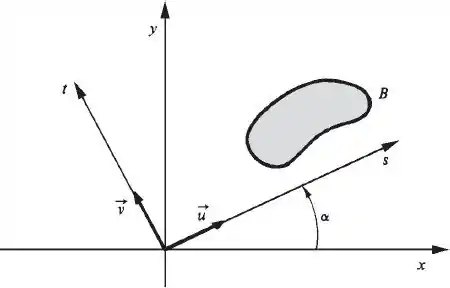
Bxy é o conjunto B olhado em relação ao sistema xy e Bst é o conjunto Bolhado em relação ao sistema st. Observe que Bxy é a imagem de Bstpela mudança de coordenadas acima.

b. Seja o centro de massa de B no sistema xy e no sistema st. Mostre que

Passo 1

Visto que o jacobiano é 1. Não deformamos o espaço. Logo nosso objeto dentro de B continua tendo o mesmo centro de massa independente do sistema de coordenadas que escolhamos. Só o que muda seria sua representação, assim podemos descobrir qual são os pontos através dessa matriz

Onde facilmente podemos substituir os valores por e

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a massa e o centro de massa da lamina que ocupa a região D e é dada pela função da densidade ρ . Dél i m i t a d ap e l a sc u r v a sy = 0ey = cos ⁡ x , - π 2 ≤ x ≤ π 2 ; ρ x , y = y é

Encontre a massa e o centro de massa da lamina que ocupa a região D e é dada pela função da densidade ρ . Dél i m i t a d ap o ry = 1 - x 2e y = 0 ; ρ x , y = k y é

Esboce a região cuja área é dada pela integral e calcule-a ∫ π / 2 π∫ 0 2 sen ⁡ θ r d r d θ

Encontre a massa e o centro de massa da lamina que ocupa a região D e é dada pela função da densidade ρ . Dél i m i t a d ap o ry = x + 2e y = x 2 ; ρ x , y = k x 2 é

Encontre a massa e o centro de massa da lamina que ocupa a região D e é dada pela função da densidade ρ . Dél i m i t a d ap e l a sc u r v a sy = e - x ,y = 0 ,x = 0 ,x = 1 ; ρ x , y = x y é