Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.4 - Ex. 2

Seja f com derivada contínua em a , b e seja P : a = x 0 < x 1 < x 2 < … <   x n = b uma partição de a ,   b . Indique por L P o comprimento da poligonal de vértices ( x 0 ,   f ( x 0 ) ) ,   ( x 1 ,   f ( x 1 ) ) ,   … ,   ( x n ,   f ( x n ) )

  1. Verifique que:

    2. lim máx  ∆ x 1 → 0 ⁡ L ( P ) = ∫ a b 1 - f ´ x 2 d x

  2. Defina comprimento do gráfico da função de f
  3. Qual uma outra motivação para tal definição? (Sugestão: aproveite a motivação para a definição de área de superfície de revolução.)

Passo 1

  1. O problema diz que P é a partição do intervalo [a, b] com x crescente, agora imagine ci é um ponto médio tal que:

    2. c i = x i + x i - 1 2

    Ou seja, o ponto médio entre esses dois pontos.

    Podemos perceber pela figura abaixo que a tangente do gráfico de função f no ponto ci vai ser igual a derivada do gráfico:

    f ´ c i = tan ⁡ α i

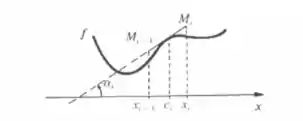
    Com isso vemos que se chamarmos o segmento M i - 1 M i da tangente do gráfico de função f   no ponto c i teremos que:

    f ´ c i = tan ⁡ α i = M i - 1 M i 2 - ∆ x i 2 ∆ x i

    Então, substituindo, teremos:

    tan ⁡ α i = M i - 1 M i 2 - ∆ x i 2 ∆ x i → M i - 1 M i   = 1 + f ´ c i 2 ∆ x i

    Isso se dá quando vemos que um dos catetos do triângulo vale 1 e o outro vale

    Agora que temos essa ideia em mente podemos aplicar para o nosso caso:

    Vamos pensar em um poligonal, que nada mais é do que uma sequência de retas que se ligam, parecidas com a imagem abaixo:

    Tendo os limites de [a, b], podemos aplicar um somatório das n seções   M i - 1 M i do gráfico e ficaremos com:

    L P = ∑ i = 1 n 1 + f ´ c i 2 ∆ x i

    Aplicando limite para ∆ x i infitesimais (para caso onde as tangentes não são tão evidentes, ou seja, casos gerais), ficaremos com:

    lim máx ∆ x i → 0   ⁡ L P = l i m m á x ∆ x i → 0   ∑ i = 1 n 1 + f ´ c i 2 ∆ x i = ∫ a b 1 + f ´ x 2 d x

    Passo 2

  2. Como vimos Podemos então definir O comprimento do gráfico f como sendo:

    3. ∫ a b 1 + f ´ x 2 d x

    Passo 3

  3. Essa definição é útil para o caso em que rotacionamos essa função em torno do eixo x, poe exemplo, pois assim conseguimos a área da superfície de revolução.

Se temos um exemplo mais simples, como o do cilindro, podemos calcular sua área de superfície abrindo o cilindro em um quadrado e calculando a área.

A área do quadrado é base X altura, no caso do cilindro fica 2 π r × h , essa altura vamos considerar como o comprimento já analisado, já o r, podemos considerar como sendo a função em cada ponto, com isso ficamos com:

A P = ∑ i = 1 n 2 π f c i 1 + f ´ c i 2 ∆ x i

Se aplicarmos limite para os casos mais gerais, teremos:

lim máx ∆ x i → 0   ⁡ A P = l i m m á x ∆ x i → 0   ∑ i = 1 n 2 π f c i 1 + f ´ c i 2 ∆ x i = ∫ a b f ( x ) 1 + f ´ x 2 d x

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para y = t gx ,0 ≤ x ≤ π 4 ; eixo x :Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do seu eixo.Trace o gráfico da curva para ver como ela é. Se puder, fa
Calcule a área da superfície gerada pela rotação, em torno do eixo x, do gráfico da função dada.d) f x = x , 1 ≤ x ≤ 4
Calcule a área da superfície gerada pela rotação, em torno do eixo x, do gráfico da função dada.b) f x = R 2 - x 2 , - R ≤ x ≤ RR0
Calcule a área da superfície gerada pela rotação, em torno do eixox, do gráfico da função dada: f x = e x + e - x 2 ,- 1 ≤ x ≤ 1
Calcule a área da superfície gerada pela rotação, em torno do eixo x, do gráfico da função dada.c) f x = x 2 , 0 ≤ x1 2