Seja .
- Determine os pontos do gráfico de em que as retas tangentes, nestes pontos, sejam paralelas ao eixo .
- Estude o sinal de .
- Calcule e .
- Utilizando as informações acima, faça um esboço do gráfico de .
Passo 1
- Vamos lá, primeiro temos que o coeficiente angular da reta é igual a derivada da função:
- Vamos agora estudar o sinal de .
- Vamos calcular os limites:
- Vamos fazer um esboço do gráfico da função utilizando as raízes e atribuindo alguns pontos aleatórios, assim temos:
Para calcular essa derivada vamos usar algumas regras, de primeira dá pra perceber que vamos usar a regra da divisão:
Temos que:
e
Vamos agora só montar na fórmula:
Passo 2
Vamos calcular , usando a regra do polinômio:
Assim:
Com além da regra do polinômio vamos usar a da função constante:
Aplicando:
Passo 3
Agora é só substituir na expressão e pronto:
Passo 4
Agora temos que para que a reta seja paralela ao eixo , o coeficiente angular da reta deve ser igual a zero, ou seja, o que acabamos de achar no passo anterior:
Por último é só substituir na equação da reta para achar os pontos:
Os pontos são:
e
Passo 5
Aqui o que nos importa é o numerador, já que o denominador vai ser sempre positivo.
Como achamos uma equação do segundo grau, temos que , como então a concavidade da parábola é voltada pra baixo.
Vamos então achar as raízes:
As raízes ficam no gráfico da seguinte forma:
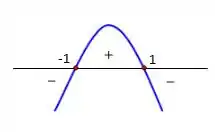
Temos então que quando:
E :
e
Passo 6
Vamos manipular um pouco a expressão, isolando no denominador:
Vamos analisar o denominador que achamos, quando aplicarmos o limite vamos ficar com , temos que vai para , assim vamos ficar com , e agora ficamos com novamente, assim o nosso limite é igual a :
Da mesma forma temos para tendendo a :
Passo 7
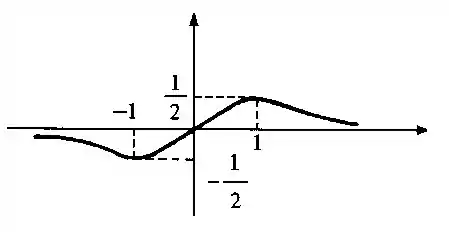
Resposta
- e
- em , em e