Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.Revisão - Ex. 63
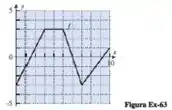
Use o gráfico de abaixo para encontrar o valor médio de no intervalo .
Passo 1
Vamos começar encontrando a equação da reta pelos pontos e ,
Substituindo o coeficiente angular na fórmula,
Passo 2
Para a representação do valor médio, usamos a expressão:
Portanto, substituindo os dados:
Resposta
Exercícios de Livros Relacionados
Expresse a quantidade dada como uma potência de e .(a) π - x (b) x 2 x , x0
Encontre a derivada usando a Fórmula (18) e verifique sua resposta calculando a integral e depois diferenciando.(a) d d x ∫ - 1 x 2 t + 1 d t (b) d d x ∫ π 1 / x s i n ( t ) d t
Seja F x = ∫ 0 x sin t t 2 + 1 d t . Encontre:(a) F ( 0 ) (b) F ' ( 0 ) (c) F ' ' ( 0 )
Use a fórmula 11 para resolver o problema de valor inicial. d y d x = x + 1 x , y 1 = 0
Use a fórmula 11 para resolver o problema de valor inicial. d y d x = 2 x 2 + 1 x , y 1 = 2