Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.3 - Ex. 47
Seja
- Encontre
- Existe
- Esboce o gráfico de .
Passo 1
Olá, caro aluno. Vamos resolver agora uma atividade de limites.
Temos aqui a função
Uma função interessante, pois conta com um modulo em seu denominador, e nos é pedido para calcularmos os limites laterais e o limite da função em .
Veja que é importante aqui nos atentarmos, qual será o denominador, já que
E
Então na hora de calcularmos os limites laterais, precisamos ter essa atenção extra.
Para calcularmos o limite
Precisamos que os limites laterais sejam iguais.
É isso, de modo geral é essa a atividade, agora vamos colocar a mão na massa.
Passo 2
- i) Vamos achar o limite
- Vamos achar o limite
- O limite
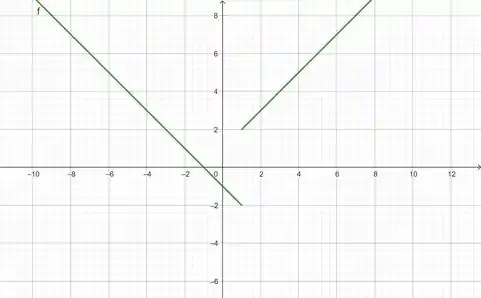
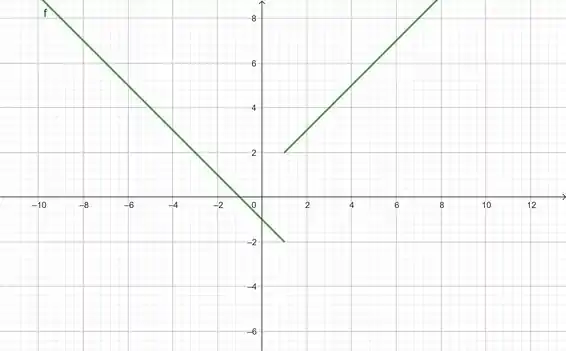
- Vamos esboçar o gráfico de
Analisando o limite pela direita, iremos trabalhar com valores infinitesimalmente maiores que 1, sendo assim:
para
Então:
Agora vamos resolver esse limite.
Vamos fatorar o numerador:
Podemos agora simplificar a expressão:
Agora ficou fácil resolver:
Passo 3
Analisando o limite pela direita, iremos trabalhar com valores infinitesimalmente menores que 1, sendo assim:
para
Então:
Vamos fatorar o numerador:
Podemos agora simplificar a expressão:
Agora ficou fácil de resolver:
Passo 4
não existe, pois, a gente comentou que para ele existe precisaríamos que os limites laterais existissem, mas como temos:
Ele não existe.
Passo 5
Para fazer isso é necessário atribuir valores a e ir encontrando seus valores associados. Aqui eu estarei utilizando o GeoGebra para isso, mas confira aí com o seu resultado:
Resposta
- i)
- não existe
ii)
