Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 32
Seja .
- Encontre . Como está relacionada a ?
- Faça um gráfico de .Como você explica a sua resposta para a parte (a)?
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo encontrar , relacionar com e esboçar os gráficos de e .
Tem ideia de como fazemos isso?
é a função inversa de ... para obter essa função inversa, igualamos e manipulamos a equação de modo que fique isolado em um lado da igualdade. Assim do outro lado da igualdade, vamos ter .
Com e em mãos, vamos analisar algumas características dessas função para esboçar seus gráficos.
Bora lá!
Passo 2
Vamos começar calculando ...
Igualando , temos
Agora isolamos em função de :
Por fim, para expressarmos como uma função de , trocamos por :
Concluímos que a função inversa de , , é igual a função , ou seja, .
Tranquilo até aqui?
Passo 3
Agora queremos esboçar os gráficos, mas como , podemos esboçar apenas um deles.
Perceba que nossa função é uma raiz... portanto, quando , já que o conteúdo da raiz vai zerar e tambem quando , .
Perceba tambem que o grau de é o mesmo que o grau da raiz... portanto, para a função vai se comportar como uma reta com inclinação negativa , já que é negativo...
Com essas informações, podemos esboçar o gráfico como...
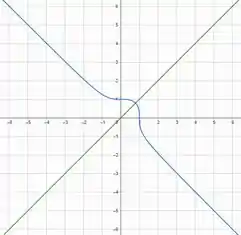
Observe que o gráfico de é simétrico em relação a uma linha imaginária , então sua reflexão sobre é ele mesmo, por isso .
E aí! entendeu tudo? Responde Aí!