Seja , .
- Encontre Como está relacionada a ?
- Identifique o gráfico de e explique a sua resposta para a parte (a) .
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá a seguinte função para o intervalo :
Queremos encontrar a função inversa .
Mas o que é essa função??
Em termos simples, se você tem uma função que mapeia elementos do conjunto para elementos do conjunto , então a função inversa mapeia elementos de de volta para elementos de .
Para calcular essa função, precisaremos isolar o em função de .
Em seguida, deveremos plotar o gráfico da função para justificarmos o que fizemos.
Bora lá?? 😉
Passo 2
- Para calcular podemos seguir um passo a passo. Primeiro escrevemos .
- Plotando o gráfico de , temos:
Assim:
Agora isolamos em função de :
Observe que como está definido no intervalor , consideramos somente a raiz positiva.
Por fim, para expressarmos como uma função de , trocamos por :
Concluímos que a função inversa de , , é igual a função , ou seja, .
Passo 3
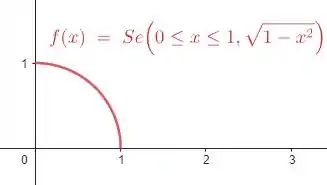
O gráfico de é a porção do círculo e , ou seja, um quarto do círculo no primeiro quadrante.
Observe que o gráfico de é simétrico em relação a uma linha imaginária , então sua reflexão sobre é ele mesmo, por isso concluímos que:
Resposta
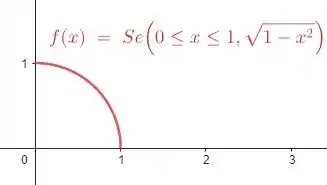
Observe que o gráfico de é simétrico em relação a uma linha imaginária , então sua reflexão sobre é ele mesmo, por isso concluímos que .