Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.7 - Ex. 5
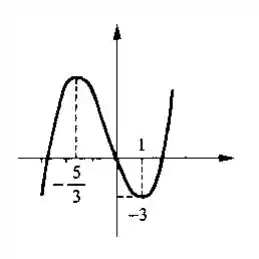
Seja .
- Estude o sinal de .
- Calcule e .
- Utilizando as informações acima, faça um esboço do gráfico de .
Passo 1
- Vamos analisar a função, ela é um polinômio, vamos ter então que usar a fórmula da derivada de polinômio e da multiplicação por constante para achar :
- Vamos calcular os limites:
- Vamos fazer um esboço do gráfico da função utilizando as raízes e atribuindo alguns pontos aleatórios, assim temos:
Do polinômio:
Da multiplicação por constante:
Agora é só aplicar, vamos lá?
Passo 2
Vamos agora estudar o sinal, como achamos uma equação do segundo grau, temos que , como então a concavidade da parábola é voltada pra cima.
Vamos então achar as raízes, usando Bhaskara, onde temos que , e :
As raízes ficam no gráfico da seguinte forma:
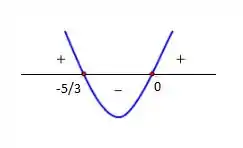
Temos então que quando:
e
E :
Passo 3
Passo 4
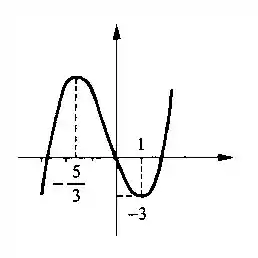
Resposta
- em e , em
- e
Exercícios de Livros Relacionados
9-12 Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.11- A aceleração é o valor absoluto da velocidade.
É dada uma função posição de uma partícula movendo-se ao longo de um eixo coordenado. Use o método do Exemplo 6 para analisar o movimento da partícula em t ≥ 0 e faça um esboço esquemático do moviment
Seja s t = 5 t 2 - 22 t a função posição de uma partícula movendo-se ao longo de um eixo coordenado, sendo s em metros e t em segundos.Encontre a velocidade escalar máxima da partícula no intervalo 1
É dada uma função posição de uma partícula movendo-se ao longo de um eixo coordenado. Use o método do Exemplo 6 para analisar o movimento da partícula em t ≥ 0 e faça um esboço esquemático do moviment
É dada uma função posição de uma partícula movendo-se ao longo de um eixo coordenado. Use o método do Exemplo 6 para analisar o movimento da partícula em t ≥ 0 e faça um esboço esquemático do moviment