Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.6 - Ex. 16

Faça o gráfico das funções y = f ( x ) dadas, explorando escalar para visualizar melhor o gráfico numa vizinhança da origem. Observando o gráfico, qual a sua conjectura sobre o lim x → 0 ⁡ f ( x ) ? Comprove analiticamente se a sua conjectura é verdadeira.

  1. f x = s e n 1 x
  2. f x = x   s e n 1 x
  3. f x = x 2 s e n 1 x
  4. f x = x 3 s e n 1 x

Passo 1

Para esboço do gráfico você pode utilizar a calculadora gráfica do GeoGebra, Symbolab, entre outras.

  1. f x = s e n 1 x

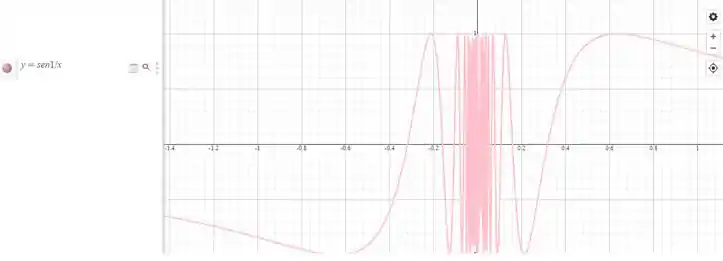    2. O gráfico para essa função é dado por:

    Observando que lim x → 0 ⁡ s e n 1 x   n ã o   e x i s t e e de forma análoga analiticamente também não.

    Passo 2

  2. f x = x   s e n 1 x

    3. O gráfico dessa função é dado por:

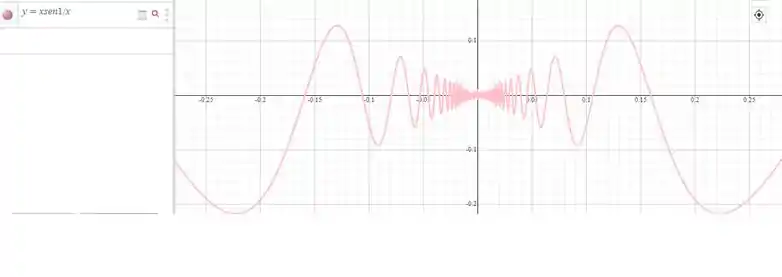
    Observamos que lim x → 0 ⁡ f x = 0 .

    Analiticamente, temos que:

    lim x → 0 ⁡ x .   s e n 1 x = 0

    Visto que a função seno é definhada para valores entre - 1   e   1 . Logo podemos escrever que:

    - 1 ≤ s e n 1 x ≤ 1 ,     ∀   x ≠ 0

    Se multiplicarmos a desigualdade acima por x > 0 , obtemos que:

    - x ≤ s e n 1 x < x ,     ∀   x > 0

    Analisando os limites laterais, temos que:

    lim x → 0 + ⁡ x = 0         e           lim x → 0 + ⁡ - x = 0

    Pela Regra do Sanduíche concluímos que:

    lim x → 0 + ⁡ x . s e n 1 x = 0

    Analogamente lim x → 0 - ⁡ x . s e n 1 x = 0 .

    Passo 3

  3. f x = x 2 .   s e n 1 x

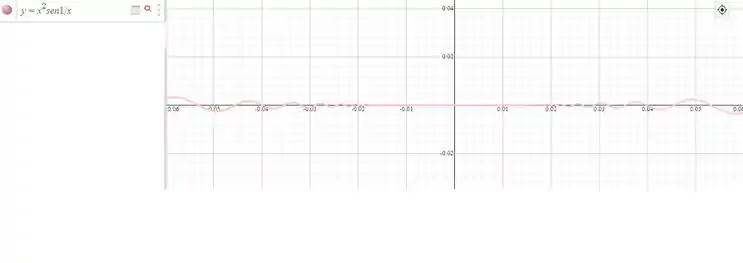    4. O gráfico dessa função é dado por:

    Observamos que lim x → 0 ⁡ f x = 0 .

    Analiticamente prova-se que lim x → 0 ⁡ x 2   s e n 1 x = 0   da mesma forma utilizada no item (b).

    Passo 4

  4. f x = x 3 .   s e n 1 x

O gráfico dessa função é dado por:

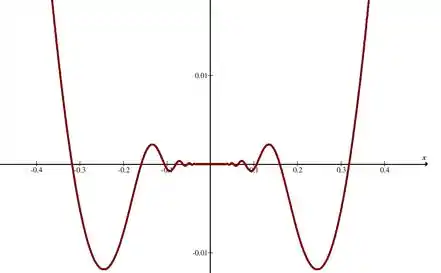
Observamos que lim x → 0 ⁡ f x = 0 .

Analiticamente prova-se que lim x → 0 ⁡ x 3   s e n 1 x = 0   da mesma forma utilizada no item (b).

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 21 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 34 )lim x → 1 ⁡ x 3 - 1 x - 1
Nos exercícios de2 1 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 2 8 )lim s → 1 ⁡ s ³ - 1 s - 1 ³
Nos exercícios de 2 1 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 30 )lim t → 3 2 ⁡ 8 t ³ - 27 4 t ² - 9 ³ ²
Nos exercícios de 21 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 33 )lim x → 0 ⁡ x + 2 - 2 x
Se f x = x ² + 5 x - 3 , ² mostre que lim x → 2 ⁡ f x = f ( 2 ) .