Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 41
41. Seja uma função constante.
(a) Use uma fórmula de Geometria para mostrar que:
(b) Mostre que o valor de qualquer soma de Riemann para sobre é . Use a definição para mostrar que
Passo 1
Para a letra a) vamos desenhar o gráfico da função e para a letra b) faremos a soma de Riemann e a definição 5.5.1 que diz:
Essa definição diz que a soma de Riemann de uma função contínua é igual a integral definida dessa função!
Passo 2
Vamos começar pela letra a) e desenhando esse gráfico, sabemos que essa é uma função constante, então seu gráfico será uma reta paralela ao eixo .
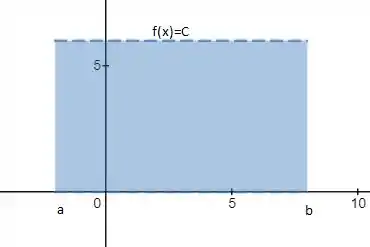
Esse gráfico é um retângulo de altura .
A base do retângulo vai de até , então mede .
A área de um retângulo é dada por base multiplicado pela altura, então:
E como a integral é numericamente igual a área líquida, podemos afirmar que:
Passo 3
Vamos agora para a Soma de Rienmann para no mesmo intervalo, temos que:
Temos que para qualquer valor de que escolhemos sempre teremos que , então a soma de Rienmann fica escrita assim:
Só que você bem lembra que um fator constante pode ser retirado do somatório, então temos que:
Esse termo acima que eu destaquei é a soma de todas as partições entre hein, lembrando que as partições são os subintervalos que eu “parto” o meu intervalo .
E a soma de todas a partições entre entre e é dada pelo comprimento do intervalo de , portanto:
Voltando para a nossa expressão e substituindo isso daqui de cima, vamos ter isso aqui:
Provamos que a soma de Rienmann dá
Utilizando a definição que eu falei la no passo 1:
Então:
Resposta
Ei, a resposta está no passo a passo :)