56. Seja uma função cuja derivada é contínua em . Ache o valor médio da inclinação da reta tangente ao gráfico de em e dê uma interpretação geométrica do resultado.

Como a questão diz que é contínua em , então é integrável nesse intervalo. Podemos usar o teorema do valor médio:

Ao isolarmos o fica assim

Assim vamos calcular o valor médio (VM) de

Substituindo na fórmula...

Como a integral da derivada de uma função é ela mesma:

Qual a interpretação disso?

Bem, o valor médio da inclinação da tangente é o valor da inclinação da secante que passa pelos ponto e . Como assim?? Desenhando o gráfico, fica melhor:

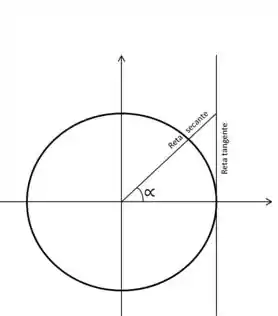
Enfim, era só pra perceber que o ângulo da tangente e da secante é o mesmo