Seja a função definida pelo gráfico:

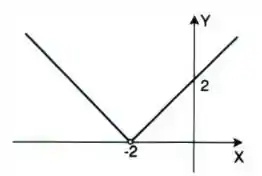
Intuitivamente, encontre se existir:

b)

Então pessoal, o que o enunciado quer é que observemos o gráfico e tentemos concluir se há algum valor para o qual a função tende quando se aproxima de pela esquerda (é isso que o termo significa). Se observamos o gráfico, à esquerda de a função tende ao valor de . Note que não estamos interessados no valor da função quando é exatamente , apenas quando se aproxima pela esquerda. Dessa forma, podemos concluir que:

E esse é o nosso resultado!