Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 15.2 - Ex. 5c
Seja uma função. Dizemos que é um ponto fixo de se , com .
Mostre que terá ponto fixo se o gráfico de interceptar a reta .
Passo 1
Vamos plotar os dois gráficos num mesmo plano:
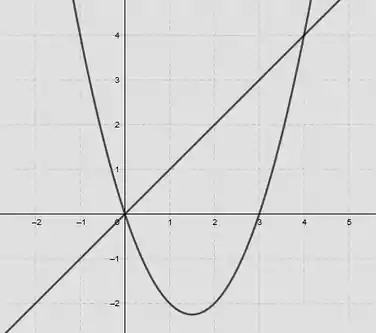
Pelo gráfico conseguimos ver que e , assim, temos esses dois pontos fixos.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Usando o teorema do valor médio provar que: sen θ - sen α ≤ θ - α , ∀θ , α ∈ R ; sin θ ≤ θ ,θ ≥ 0 .
A função f x = x 2 3 - 1 é tal que f - 1 = f 1 = 0 . Por que ela não verifica o Teorema de Rolle no intervalo [ - 1,1 ] ?
Em cada um dos seguintes casos, verificar se o Teorema do Valor Médio se aplica. Em caso afirmativo, achar um número c em ( a , b ) , tal que f ' c = f b - f a b - a Interpretar geometricamente.(h) f
Em cada um dos seguintes casos, verificar se o Teorema do Valor Médio se aplica. Em caso afirmativo, achar um número c em ( a , b ) , tal que f ' c = f b - f a b - a Interpretar geometricamente.(c) f
Em cada um dos seguintes casos, verificar se o Teorema do Valor Médio se aplica. Em caso afirmativo, achar um número c em ( a , b ) , tal que f ' c = f b - f a b - a Interpretar geometricamente.(d) f