Seja uma função linear. Use o gráfico de para explicar por que o valor médio de em é
Passo 1
Esse é o gráfico de uma função linear genérica:
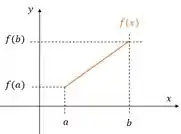
Vamos tentar usar ele para provar o que o enunciado pediu. Vem comigo!
Passo 2
A fórmula do valor médio de uma função é:
Como essa integral é uma área, podemos interpretar a área abaixo do nosso gráfico como um triângulo e um retângulo, e reescrever essa integral assim:
O valor médio fica:
Passo 3
Como a função é linear, valem relações de linearidade:
Então podemos fazer o caminho inverso do que fizemos nesse exemplinho aí de cima, com o nosso valor de
Que é exatamente o que ele pede para provar!
Resposta
Prova nos passos